题目内容
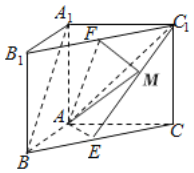
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1,且E,F分别是BC,B1C1中点.

(1)求证:A1B∥平面AEC1;
(2)求直线AF与平面AEC1所成角的正弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1) 连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 再证明
再证明![]() 即可.
即可.
(2) 作![]() 于
于![]() ,连接
,连接![]() ,再证明
,再证明![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角再求解即可.
所成角再求解即可.
证明:(1)连接A1C交AC1于点O,连接EO
∵ACC1A1为正方形,∴O为A1C中点,
又E为CB中点,∴EO为△A1BC的中位线,
∴EO∥A1B,
又EO平面AEC1,A1B平面AEC1,
∴A1B∥平面AEC1.
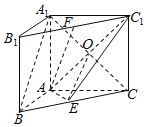
解:(2)作FM⊥EC1于M,连接AM,
∵AB=AC,E为BC的中点,
∴AE⊥BC,
又∵平面ABC⊥平面BCC1B1,且平面ABC⊥平面BCC1B1=BC,
AE平面ABC,∴AE⊥平面BCC1B1,
而AE平面AEC1,
∴平面AEC1⊥平面BCC1B1,∴FM⊥平面AEC1,
∴∠FAM即为直线AF与平面AEC1所成角,
设AB=AC=AA1=1,
则在Rt△AFM中,
在![]() 中,
中,![]() ,
,![]() ,
,![]()
因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
在![]() 中
中![]() ,
,![]() ,故
,故![]() ,
,
∴直线AF与平面AEC1所成角的正弦值sin∠FAM![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目