题目内容
18.定义在(0,+∞)上的函数f(x)满足f(mn)=f(m)+f(n)(m,n>0),且当x>1时,f(x)>0.(1)求f(1)的值;
(2)求证:f($\frac{x}{y}$)=f(x)-f(y);
(3)求证:f(x)在(0,+∞)上是增函数;
(4)若f(2)=1,解不等式f(x+2)-f(2x)>2;
(5)比较f($\frac{m+n}{2}$)与$\frac{f(m)+f(n)}{2}$的大小.
分析 (1)令m=m=1,即可求f(1)的值;
(2)根据抽象函数的关系即可证明f($\frac{x}{y}$)=f(x)-f(y);
(3)根据函数单调性的定义即可证明f(x)在(0,+∞)上是增函数;
(4)若f(2)=1,求出f(4)=2,将不等式进行转化即可解不等式f(x+2)-f(2x)>2;
(5)利用作差法即可比较f($\frac{m+n}{2}$)与$\frac{f(m)+f(n)}{2}$的大小.
解答 解:(1)∵f(mn)=f(m)+f(n)(m,n>0),
∴令m=n=1,可得f(1)=f(1)+f(1)=2f(1),
则f(1)=0.
(2)∵f(x)=f($\frac{x}{y}$•y)=f($\frac{x}{y}$)+f(y),
∴f($\frac{x}{y}$)=f(x)-f(y);
(3)证明:设0<x1<x2,则$\frac{{x}_{2}}{{x}_{1}}$>1,则f($\frac{{x}_{2}}{{x}_{1}}$)>0,
f(x2)-f(x1)=f($\frac{{x}_{2}}{{x}_{1}}$•x1)-f(x1)=f($\frac{{x}_{2}}{{x}_{1}}$)>0,
即f(x2)>f(x1),
则f(x)在(0,+∞)为增函数.
(4)若f(2)=1,则f(2)+f(2)=f(4)=2,
则不等式f(x+2)-f(2x)>2等价为f(x+2)-f(2x)>f(4);
即f(x+2)>f(2x)+f(4)=f(8x);
则满足$\left\{\begin{array}{l}{x+2>0}\\{2x>0}\\{x+2>8x}\end{array}\right.$,即$\left\{\begin{array}{l}{x>-2}\\{x>0}\\{x<\frac{2}{7}}\end{array}\right.$,
解得0<x<$\frac{2}{7}$.
(5)∵2f($\frac{m+n}{2}$)=f(($\frac{m+n}{2}$)2)≥f(($\sqrt{mn}$)2)=f(mn)=f(m)+f(n),
∴f($\frac{m+n}{2}$)≥$\frac{f(m)+f(n)}{2}$.
点评 本题主要考查抽象函数的应用,利用抽象函数的关系以及赋值法是解决本题的关键.考查学生的运算和推理能力.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于y=x对称 |
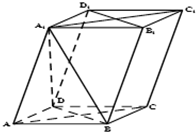 如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.
如图,平行六面体体ABCD-A1B1C1D1中,所有棱长均为1,且∠BAD=∠A1AB=∠A1AC=60°.