Question

9．某窗的形状是由半圆置于矩形上面所形成的，若此窗框的周长L为一定，试确定半圆的半径和矩形的高，使通过的光线最充足．

Answer 1

分析 下部为矩形，上部为半圆形的框架窗户，设圆的半径为x米，分别计算其面积，可得框架围成的面积y与x的函数式，进一步利用配方法，可求函数的最值

解答 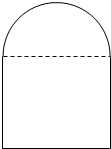解：设圆的半径为x米，框架围成的面积为y，
则矩形的一条边为2x米，另一条边为$\frac{1}{2}$（L-2x-πx）米，
y=$\frac{1}{2}$πx²+$\frac{1}{2}$（L-2x-πx）•2x
=-（2+$\frac{π}{2}$）x²+Lx=-$\frac{4+π}{2}$（x-$\frac{L}{π+4}$）²+$\frac{{L}^{2}}{2π+8}$．
∴该窗户上半圆的半径为$\frac{L}{π+4}$，下半矩形的高$\frac{L}{π+4}$，
才能使通过的光线最充足．

点评 此题考查二次函数的应用，注意利用圆的面积和矩形的面积计算公式建立函数模型解决问题．