题目内容
【题目】某校高一（2）班共有60名同学参加期末考试，现将其数学学科成绩（均为整数）分成六个分数段[40，50），[50，60），…，[90，100]，画出如如图所示的部分频率分布直方图，请观察图形信息，回答下列问题：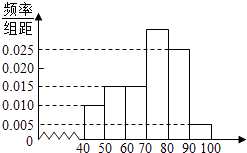 
（1）求70～80分数段的学生人数；
（2）估计这次考试中该学科的优分率（80分及以上为优分）、中位数、平均值；
（3）现根据本次考试分数分成下列六段（从低分段到高分段依次为第一组、第二组、…、第六组）为提高本班数学整体成绩，决定组与组之间进行帮扶学习．若选出的两组分数之差大于30分（以分数段为依据，不以具体学生分数为依据），则称这两组为“最佳组合”，试求选出的两组为“最佳组合”的概率．
【答案】
（1）解：根据题意得：60×[1﹣（0.005+0.010+0.015×2+0.025）×10]=18（人）
（2）解：成绩在80分及以上的学生有60×（0.005+0.025）×10=18（人），
∴估计这次考试中该学科的优分率为 
×100%=30%；
该学科40～50分数段人数为60×0.01×10=6（人）；50～60分数段人数为60×0.015×10=9（人）；60～70分数段人数为60×0.015×10=9（人）；
70～80分数段人数为18人；80～90分数段人数为60×0.025×10=15（人）；90～100分数段人数为60×0.005×10=3（人）；
∴估计这次考试中位数为70～80分数段，即75分；
平均值为 
（45×6+55×9+65×9+75×18+85×15+95×3）=71（分）
（3）解：所有的组合数：（1，2），（1，3），（1，4），（1，5），（1，6），（2，3），（2，4），（2，5），（2，6），（3，4），（3，5），（3，6），（4，5），（4，6），（5，6），即n=5+4+3+2+1=15，
符合“最佳组合”条件的有：（1，4），（1，5），（1，6），（2，5），（2，6），（3，6），即m=6，
则P= 
= 
= 
【解析】（1）根据条形统计图1求出70～80分数段的学生人数频率，乘以60即可确定出人数；（2）求出80分及以上学生人数，确定出优生率，找出中位数，平均值即可；（3）根据题意得出所有等可能的情况数，找出“最佳组合”数，即可确定出选出的两组为“最佳组合”的概率．
