题目内容
(本小题满分14分)已知 ,
,
1)若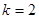 ,求方程
,求方程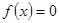 的解;
的解;
2)若对 在
在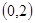 上有两个零点,求
上有两个零点,求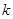 的取值范围.
的取值范围.
(1)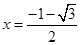 或
或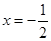 。(2)
。(2)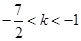 。
。
解析试题分析:(1)当k=2时, 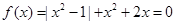
① 当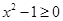 时,
时,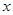 ≥1或
≥1或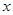 ≤-1时,方程化为2
≤-1时,方程化为2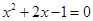
解得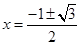 ,因为
,因为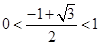 ,舍去,所以
,舍去,所以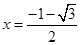 .
.
②当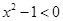 时,-1<
时,-1<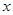 <1时,方程化为
<1时,方程化为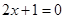 ,解得
,解得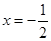 ,
,
由①②得当k=2时,方程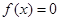 的解所以
的解所以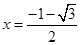 或
或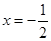 .
.
(II)解:不妨设0<x1<x2<2,
因为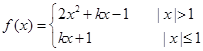
所以 在(0,1]是单调函数,故
在(0,1]是单调函数,故 =0在(0,1]上至多一个解,
=0在(0,1]上至多一个解,
若1<x1<x2<2,则x1x2=-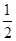 <0,故不符题意,因此0<x1≤1<x2<2.
<0,故不符题意,因此0<x1≤1<x2<2.
由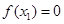 得
得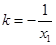 , 所以
, 所以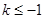 ;
;
由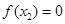 得
得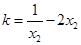 , 所以
, 所以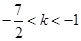 ;
;
故当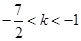 时,方程
时,方程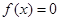 在(0,2)上有两个解.
在(0,2)上有两个解.
考点:含绝对值的函数性质;一元二次函数的性质;函数的零点。
点评:本题主要考查方程的根与函数的零点的关系,以及分类讨论的数学思想。含绝对值的有关问题,常要分类讨论,在分类讨论时,要做到不重不漏。同时也考查了学生分析问题、解决问题的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 。
。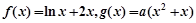 .
. ,求
,求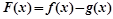 的单调区间;
的单调区间; 恒成立,求
恒成立,求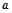 的取值范围.
的取值范围.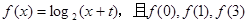 成等差数列,点
成等差数列,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点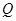 的轨迹是函数
的轨迹是函数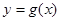 的图像。
的图像。 的不等式
的不等式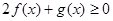 ;
;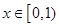 时,总有
时,总有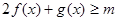 恒成立,求
恒成立,求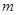 的取值范围。
的取值范围。 且
且 ,
, 的取值范围;
的取值范围;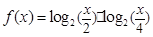 的最大值和最小值及对应的x值。
的最大值和最小值及对应的x值。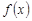 =
=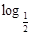 (ex-1)。
(ex-1)。 上的函数
上的函数 满足
满足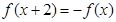 ,且当
,且当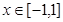 时,
时,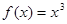 ,
, 上的表达式;
上的表达式;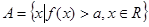 ,且
,且 ,求实数
,求实数 的取值范围。
的取值范围。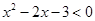 的解集为
的解集为 ,不等式
,不等式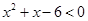 的解集为
的解集为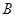 。
。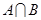 ;
; 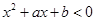 的解集为
的解集为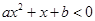 的解集。
的解集。