题目内容
(本题满分13分)
已知函数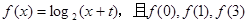 成等差数列,点
成等差数列,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点 关于原点的对称点
关于原点的对称点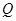 的轨迹是函数
的轨迹是函数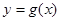 的图像。
的图像。
(1)解关于 的不等式
的不等式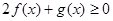 ;
;
(2)当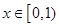 时,总有
时,总有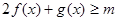 恒成立,求
恒成立,求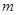 的取值范围。
的取值范围。
(1)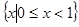 (2)
(2)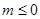
解析试题分析:解:由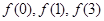 成等差数列,得
成等差数列,得 ,
,
即 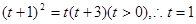
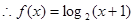 …… 2分
…… 2分
由题意知: 、
、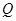 关于原点对称,设
关于原点对称,设 函数
函数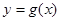 图像上任一点,则
图像上任一点,则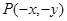 是
是 上的点,所以
上的点,所以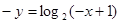 ,于是
,于是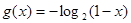 …… 4分
…… 4分
(1) 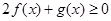
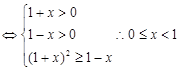
此不等式的解集是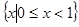 …… 6分 (2)
…… 6分 (2)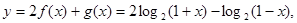 当
当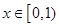 时
时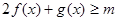 恒成立,
恒成立,
即在当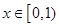 时
时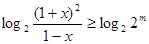 恒成立,即
恒成立,即 , …… 8分
, …… 8分
设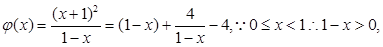


 …… 13分
…… 13分
考点:动点的轨迹方程及解不等式,不等式与函数的转化
点评:本题第一问用到的是相关点法求轨迹方程,第二问将不等式恒成立转化为求函数最值,进而利用导数求其最值

练习册系列答案
相关题目
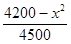 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).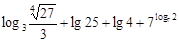
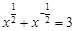 ,求
,求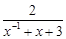 的值.
的值.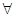 x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;
x∈(0,+∞)均有f (x)≥h(x)≥g(x)成立,求实数k的取值范围;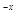 +1≤0恒成立,求实数a的取值范围.
+1≤0恒成立,求实数a的取值范围. 个月的利润
个月的利润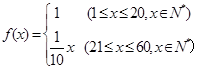 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第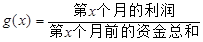 ,例如:
,例如: .
.  求
求 ; (Ⅱ)求第
; (Ⅱ)求第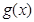 ;
;
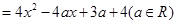 ,若方程
,若方程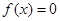 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于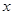 的不等式
的不等式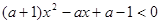 是否对一切实数
是否对一切实数 ,
,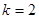 ,求方程
,求方程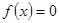 的解;
的解; 在
在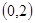 上有两个零点,求
上有两个零点,求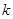 的取值范围.
的取值范围.
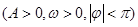 ,在同一周期内,
,在同一周期内,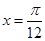 时,
时, 取得最大值
取得最大值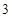 ;当
;当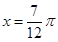 时,
时,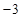 .
.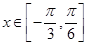 时,函数
时,函数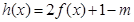 有两个零点,求实数
有两个零点,求实数 的取值范围.
的取值范围.