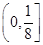题目内容
若圆 与圆
与圆 的公共弦长为
的公共弦长为 ,则
,则 的值为
的值为
A. | B.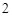 | C. | D.无解 |
A
解析试题分析:圆 的圆心为原点O,半径
的圆心为原点O,半径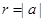 .
.
将圆 与圆
与圆 相减,
相减,
可得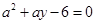 ,
,
即得两圆的公共弦所在直线方程为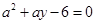 .
.
原点O到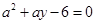 的距离d=|
的距离d=|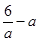 |,
|,
设两圆交于点A、B,根据勾股定理可得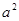 =(
=( )2+(
)2+(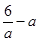 )2∴
)2∴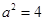 ,∴
,∴ =±2.故选A..
=±2.故选A..
考点:圆与圆的位置关系.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
若圆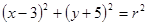 上的点到直线
上的点到直线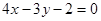 的最近距离等于1,则半径
的最近距离等于1,则半径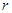 的值为( )
的值为( )
A.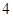 | B.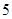 | C.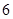 | D.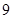 |
已知条件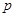 :
: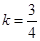 ,条件
,条件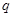 :直线
:直线 与圆
与圆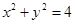 相切,则
相切,则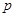 是
是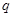 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
若圆C: 关于直线
关于直线 对称,则由点
对称,则由点 向圆所作的切线长的最小值是( )
向圆所作的切线长的最小值是( )
| A.2 | B. 4 | C.3 | D.6 |
直线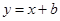 与曲线
与曲线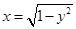 有且仅有1个公共点,则b的取值范围是( )
有且仅有1个公共点,则b的取值范围是( )
A.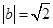 | B. 或 或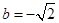 |
C.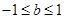 | D.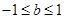 或 或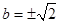 |
点 到圆
到圆 上的点的距离的最小值是( )
上的点的距离的最小值是( )
| A.1 | B.4 | C.5 | D.6 |
若直线 始终平分圆
始终平分圆 的周长,则
的周长,则 的取值范围是( )
的取值范围是( )
| A.(0,1) | B.(0,-1) | C.(-∞,1) | D.(-∞,-1) |
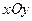 中,直线
中,直线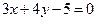 与圆
与圆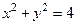 相交于A、B两点,则弦AB的长等于 ( )
相交于A、B两点,则弦AB的长等于 ( )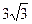 B.
B.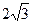 C.
C. D.1
D.1