题目内容
若直线
始终平分圆
的周长，则
的取值范围是( )
| A．(0,1) | B．(0，－1) | C．(－∞，1) | D．(－∞，－1) |
C
解析试题分析：∵直线平分圆，
∴圆心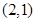
在直线
上，即
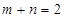，可化为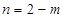
，∴
．
∴
，
∵，∴
．
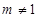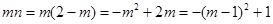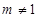考点：1.直线与圆的位置关系；2.二次函数求最值．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
若圆
与圆
的公共弦长为
，则
的值为
A． | B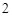． | C． | D．无解 |
如果圆
上总存在两个点到原点的距离为
则实数a的取值范围是
A． | B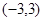． | C．[-1，1] | D． |
已知平面
∥平面
，点P
平面,平面、间的距离为8，则在内到点P的距离为10的点的轨迹是（ ）
| A．一个圆 | B．四个点 |
| C．两条直线 | D．两个点 |
若圆C的半径为1，圆心在第一象限，且与直线4x-3y=0和x轴都相切，则该圆
的标准方程是 （ ）
| A．（x-2）2+（y-1）2=1 |
| B．（x-2）2+（y+1）2=1 |
| C．（x+2）2+（y-1）2=1 |
| D．（x-3）2+（y-1）2=1 |
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A．x2+y2=2 | B．x2+y2=4 |
| C．x2+y2=2(x≠±2) | D．x2+y2=4(x≠±2) |
圆心在y轴上,半径为1,且过点(1,2)的圆的方程为( )
| A．x2+(y-2)2=1 | B．x2+(y+2)2=1 |
| C．(x-1)2+(y-3)2=1 | D．x2+(y-3)2=1 |
从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为( )
| A．π | B．2π | C．4π | D．6π |
若点P(1,1)是圆x2＋(y－3)2＝9的弦AB的中点，则直线AB的方程为( )
| A．x－2y＋1＝0 | B．x＋2y－3＝0 |
| C．2x＋y－3＝0 | D．2x－y－1＝0 |