题目内容
已知条件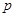 :
: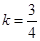 ,条件
,条件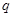 :直线
:直线 与圆
与圆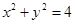 相切,则
相切,则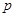 是
是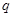 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
C
解析试题分析:由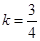 ,可得直线
,可得直线 为
为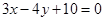 .所以圆心(0,0)到该直线的距离
.所以圆心(0,0)到该直线的距离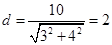 等于半径,所以直线与圆相切.所充分性成立.当直线
等于半径,所以直线与圆相切.所充分性成立.当直线 与圆
与圆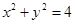 相切,可解得
相切,可解得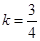 .所以必要性成立.综上
.所以必要性成立.综上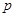 是
是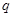 的充要条件.
的充要条件.
考点:1.充分必要条件.2.直线与圆的位置关系.3.二次方程的解法.

练习册系列答案
相关题目
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.外离 | B.外切 | C.相交 | D.内切 |
若圆 与圆
与圆 的公共弦长为
的公共弦长为 ,则
,则 的值为
的值为
A. | B.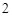 | C. | D.无解 |
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆
的标准方程是 ( )
| A.(x-2)2+(y-1)2=1 |
| B.(x-2)2+(y+1)2=1 |
| C.(x+2)2+(y-1)2=1 |
| D.(x-3)2+(y-1)2=1 |
圆x2+y2+2x=0和x2+y2﹣4y=0的公共弦的长度为( )
A.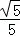 | B. | C. | D. |
直线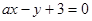 与圆
与圆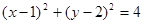 相交于
相交于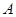 、
、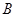 两点且
两点且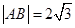 ,则a的值为( )
,则a的值为( )
| A.3 | B.2 | C.1 | D.0 |
从原点向圆x2+y2-12y+27=0作两条切线,则该圆夹在两条切线间的劣弧长为( )
| A.π | B.2π | C.4π | D.6π |
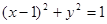 上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是( )
上的动点,PA是圆的切线且|PA|=1,则P点的轨迹方程是( )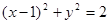
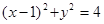
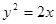
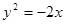
 和圆:
和圆: 交于A、B两点,则AB的垂直平分线的方程是( ).
交于A、B两点,则AB的垂直平分线的方程是( ). B.
B. C.
C.  D.
D.