题目内容
若圆C:
关于直线
对称，则由点
向圆所作的切线长的最小值是（ ）
| A．2 | B． 4 | C．3 | D．6 |
解析试题分析：即
，
由已知，直线过圆心
，即
，
由平面几何知识知，为使由点向圆所作的切线长的最小，只需圆心与直线
上的点连线段最小，所以，切线长的最小值为
，
故选.
考点：圆的几何性质，点到直线距离公式.
练习册系列答案
金博士一点全通系列答案
相关题目
直线
与圆
的位置关系是（ ）
| A．外离 | B．外切 | C．相交 | D．内切 |
若圆
与圆
的公共弦长为
，则
的值为
A． | B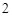． | C． | D．无解 |
已知动圆
与圆
和圆
都外切,则动圆圆心的轨迹是（ ）
| A．圆 | B．椭圆 | C．双曲线 | D．双曲线的一支 |
若圆
上的任意一点关于直线
的对称点仍在圆上，则
最小值为（ ）
A． | B． | C． | D． |
已知圆C的方程为
，若以直线
上任意一点为圆心，以l为半径的圆与圆C没有公共点，则k的整数值是（ ）
A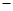． l | B．0 | C．1 | D．2 |
圆x2+y2+2x=0和x2+y2﹣4y=0的公共弦的长度为（ ）
A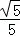． | B． | C． | D． |
已知圆C1：(x＋1)2＋(y－1)2＝1，圆C2与圆C1关于直线x－y－1＝0对称，则圆C2的方程为( )
| A．(x－1)2＋(y＋1)2＝1 |
| B．(x＋2)2＋(y－2)2＝1 |
| C．(x＋1)2＋(y－1)2＝1 |
| D．(x－2)2＋(y＋2)2＝1 |
已知M(-2,0),N(2,0),则以MN为斜边的直角三角形的直角顶点P的轨迹方程为( )
| A．x2+y2=2 | B．x2+y2=4 |
| C．x2+y2=2(x≠±2) | D．x2+y2=4(x≠±2) |