题目内容
已知f(x)、g(x)都是定义在R上的函数,g(x)≠0, ,且f′(x)g(x)>f(x)g′(x),(a>0,且a≠1),
,且f′(x)g(x)>f(x)g′(x),(a>0,且a≠1),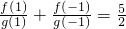 .若数列
.若数列 的前n项和大于62,则n的最小值为
的前n项和大于62,则n的最小值为
- A.6
- B.7
- C.8
- D.9
A
分析:根据导数不等式可知函数 的单调性,从而确定a的取值范围,然后根据条件求出a的值,从而可判定数列
的单调性,从而确定a的取值范围,然后根据条件求出a的值,从而可判定数列 是等比数列,可求出其前n项和,然后求出满足条件的n,由此可得答案.
是等比数列,可求出其前n项和,然后求出满足条件的n,由此可得答案.
解答:∵f′(x)g(x)>f(x)g′(x),
∴[ ]′=
]′=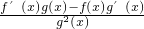 >0,即
>0,即 单调递增,
单调递增,
又 =ax,故a>1.
=ax,故a>1.
所以由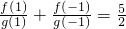 ,即a+a-1=
,即a+a-1= ,解得a=2.
,解得a=2.
所以数列 是以2为首项,2为公比的等比数列,其前n项和Sn=
是以2为首项,2为公比的等比数列,其前n项和Sn=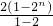 =2(2n-1),
=2(2n-1),
由Sn>62即2(2n-1)>62,解得n≥6,
所以n的最小值为6.
故选A.
点评:本题主要考查了利用导数研究函数的单调性,以及等比数列的前n项和,同时考查了运算求解能力,考查计算能力和转化得思想,属于基础题.
分析:根据导数不等式可知函数
 的单调性,从而确定a的取值范围,然后根据条件求出a的值,从而可判定数列
的单调性,从而确定a的取值范围,然后根据条件求出a的值,从而可判定数列 是等比数列,可求出其前n项和,然后求出满足条件的n,由此可得答案.
是等比数列,可求出其前n项和,然后求出满足条件的n,由此可得答案.解答:∵f′(x)g(x)>f(x)g′(x),
∴[
 ]′=
]′=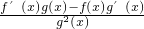 >0,即
>0,即 单调递增,
单调递增,又
 =ax,故a>1.
=ax,故a>1.所以由
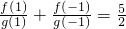 ,即a+a-1=
,即a+a-1= ,解得a=2.
,解得a=2.所以数列
 是以2为首项,2为公比的等比数列,其前n项和Sn=
是以2为首项,2为公比的等比数列,其前n项和Sn=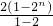 =2(2n-1),
=2(2n-1),由Sn>62即2(2n-1)>62,解得n≥6,
所以n的最小值为6.
故选A.
点评:本题主要考查了利用导数研究函数的单调性,以及等比数列的前n项和,同时考查了运算求解能力,考查计算能力和转化得思想,属于基础题.

练习册系列答案
相关题目