题目内容
将边长为 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?小正方形的边长为,容积最大为
试题分析:设小正方形的边长为x,则盒底的边长为a-2x,
∴方盒的体积
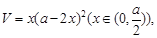 ……………………………………4分
……………………………………4分
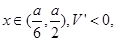 ……………………………………10分
……………………………………10分∴函数V在点x=处取得极大值,由于问题的最大值存在,
∴V()=即为容积的最大值,此时小正方形的边长为.…………………12分
点评:将实际问题转化为单存的数学问题时要注意自变量x的取值范围,本题首先找到边长与容积的关系式,通过导数即可求其最大值

练习册系列答案
相关题目
 元(
元( 元.(14分)
元.(14分)
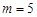 时,求
时,求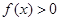 的解集
的解集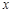 的不等式
的不等式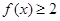 的解集是
的解集是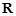 ,求
,求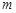 的取值范围
的取值范围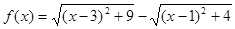 ,则
,则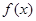 的最大值是 .
的最大值是 .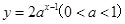 的图象一定过点( )
的图象一定过点( ) 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意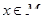 ,有
,有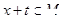 ,且
,且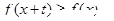 ,则称
,则称 上的3级类增函数
上的3级类增函数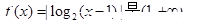 上的1级类增函数
上的1级类增函数 上的
上的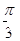 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2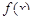 是定义
是定义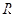 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意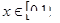 ,恒有
,恒有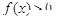 ;2.对任意
;2.对任意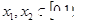 ,恒有
,恒有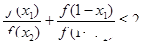 ;3. 对任意
;3. 对任意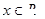 ,
,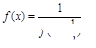 ,若函数
,若函数 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为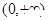 。
。 .
. ,函数
,函数 是R上的奇函数,当
是R上的奇函数,当 时
时 ,(i)求实数
,(i)求实数 与
与
 时,求
时,求 的两根中,一根属于区间
的两根中,一根属于区间 ,另一根属于区间
,另一根属于区间 ,求实数
,求实数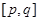 上有意义的两个函数
上有意义的两个函数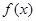 和
和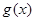 ,如果对于任意的
,如果对于任意的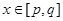 ,都有
,都有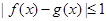 ,则称
,则称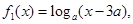 ,
,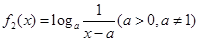 ,且
,且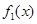 与
与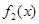 在
在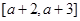 都有意义.
都有意义.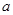 的取值范围;
的取值范围; 在
在 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.