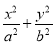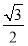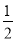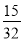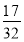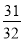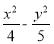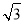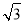题目内容
过双曲线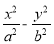
＝1(a>0，b>0)的左焦点F(－c,0)作圆x2＋y2＝a2的切线，切点为E，延长FE交抛物线y2＝4cx于点P，O为原点，若
，则双曲线的离心率为( )．
A. 
B. 
C. 
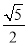D. 
A
【解析】因为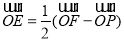
，所以E是FP的中点．设双曲线的右焦点为F1，则F1也是抛物线的焦点．连接PF1，则|PF1|＝2a，且PF⊥PF1，所以|PF|＝
＝2b，设P(x，y)，过点F作x轴的垂线l，过点P作l的垂线，垂足为M，点P到该垂线的距离为2a，则x＋c＝2a，则x＝2a－c，在Rt△PMF中，由勾股定理得y2＋4a2＝4b2，即4c(2a－c)＋4a2＝4(c2－a2)，解得e＝
.
练习册系列答案
相关题目
