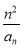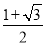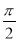题目内容
如图，椭圆
＝1(a>b>0)的左、右焦点为F1，F2，上顶点为A，离心率为
，点P为第一象限内椭圆上的一点，若S△PF1A∶S△PF1F2＝2∶1，则直线PF1的斜率为________．
【解析】因为椭圆的离心率为
，所以e＝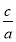
＝，即a＝2c，则A(0，b)，F2(c,0)，
设直线PF1的斜率为k(k>0)，则直线PF1的方程为y＝k(x＋c)，因为S△PF1A∶S△PF1F2＝2∶1，即S△PF1A＝2S△PF1F2，即·|PF1|·
＝2×·|PF1|·
，所以|kc－b|＝4|kc|，解得b＝－3kc(舍去)或5kc，又a2＝b2＋c2，即a2＝25k2c2＋c2，所以4c2＝25k2c2＋c2，解得k2＝
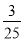，所以k＝
.
练习册系列答案
相关题目
