题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() ,其中
,其中![]() 是自然对数的底数,讨论
是自然对数的底数,讨论![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上单调递增,无极值;当
上单调递增,无极值;当![]() 时,
时,![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减,极大值为
单调递减,极大值为![]() ,极小值为
,极小值为![]() .
.
【解析】
(1)求出函数的导数,计算![]() ,
,![]() 的值,求出切线方程即可;
的值,求出切线方程即可;
(2)求出函数的导数,根据函数的单调性求出函数的最小值,从而求出函数的极值即可.
(1)由题意![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() ,
,
因此曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() ,
,
即![]() .
.
(2)因为![]() ,
,
所以![]()
![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
所以当![]() 时,
时,![]() ,
,
也就说,对于![]() 恒有
恒有![]() .
.
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,令
时,令![]() ,可得
,可得![]() .当
.当![]() 或
或![]() ,
,
![]() ,
,![]() 单调递增,
单调递增,
当![]() ,
,![]() ,
,![]() 单调递减;
单调递减;
因此,当![]() 时,
时,![]() 取极大值
取极大值![]() ;
;
当![]() 时,
时,![]() 取极小值
取极小值![]() .
.
综上所述:
当![]() 时,
时,![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,
时,![]() 在
在![]() 和
和![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
函数既有极大值,又有极小值,
极大值为![]() ,
,
极小值为![]() .
.

 科学实验活动册系列答案
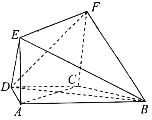
科学实验活动册系列答案【题目】有一个同学家开了一个奶茶店,他为了研究气温对热奶茶销售杯数的影响,从一季度中随机选取5天,统计出气温与热奶茶销售杯数,如表:
气温 | 0 | 4 | 12 | 19 | 27 |
热奶茶销售杯数 | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求热奶茶销售杯数关于气温的线性回归方程![]() (
(![]() 精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
精确到0.1),若某天的气温为15oC,预测这天热奶茶的销售杯数;
(Ⅱ)从表中的5天中任取一天,若已知所选取该天的热奶茶销售杯数大于120,求所选取该天热奶茶销售杯数大于130的概率.
参考数据:![]() ,
,![]() .参考公式:
.参考公式: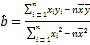 ,
,![]()
【题目】某![]() 手机专卖店对某市市民进行
手机专卖店对某市市民进行![]() 手机认可度的调查,在已购买
手机认可度的调查,在已购买![]() 手机的1000名市民中,随机抽取100名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
手机的1000名市民中,随机抽取100名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
分组(岁) | 频数 |
| 5 |
|
|
| 35 |
|
|
| 10 |
合计 | 100 |
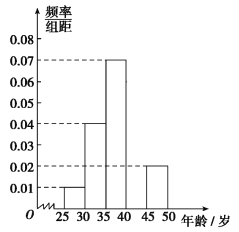
(1)求频数分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这100名市民中,从年龄在![]() 、
、![]() 内的市民中用分层样的方法抽取5人参加
内的市民中用分层样的方法抽取5人参加![]() 手机宣传活动,现从这5人中随机选取2人各赠送一部
手机宣传活动,现从这5人中随机选取2人各赠送一部![]() 手机,求这2人中恰有1人的年龄在
手机,求这2人中恰有1人的年龄在![]() 内的概率.
内的概率.
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 |
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某市12月1日-20日AQI指数变化趋势:

下列叙述正确的是( )
A.这20天中AQI指数值的中位数略高于100
B.这20天中的中度污染及以上的天数占![]()
C.该市12月的前半个月的空气质量越来越好
D.总体来说,该市12月上旬的空气质量比中旬的空气质量好