题目内容
【题目】某![]() 手机专卖店对某市市民进行
手机专卖店对某市市民进行![]() 手机认可度的调查,在已购买
手机认可度的调查,在已购买![]() 手机的1000名市民中,随机抽取100名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
手机的1000名市民中,随机抽取100名,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如下:
分组(岁) | 频数 |
| 5 |
|
|
| 35 |
|
|
| 10 |
合计 | 100 |
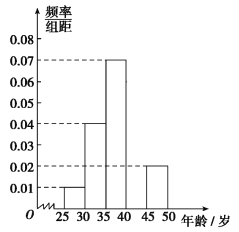
(1)求频数分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这100名市民中,从年龄在![]() 、
、![]() 内的市民中用分层样的方法抽取5人参加
内的市民中用分层样的方法抽取5人参加![]() 手机宣传活动,现从这5人中随机选取2人各赠送一部
手机宣传活动,现从这5人中随机选取2人各赠送一部![]() 手机,求这2人中恰有1人的年龄在
手机,求这2人中恰有1人的年龄在![]() 内的概率.
内的概率.
【答案】(1)见解析;(2)![]()
【解析】
(1)由频数分布表和频率分布直方图,可得![]() ,解得
,解得![]() ,进而可求得年龄在
,进而可求得年龄在![]() 内的人数对应的
内的人数对应的![]() ,即可补全频率分布直方图.
,即可补全频率分布直方图.
(2)由频数分布表,可得年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,记为
,记为![]() ,年龄在
,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,分别记为
,分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,利用列举法求得基本事件的总数,以及事件 “恰有1人的年龄在
,利用列举法求得基本事件的总数,以及事件 “恰有1人的年龄在![]() 内”所包含的基本事件的个数,利用古典概型及其概率的计算公式,即可求解.
内”所包含的基本事件的个数,利用古典概型及其概率的计算公式,即可求解.
(1)由频数分布表和频率分布直方图可知,![]() ,解得
,解得![]() .
.
频率分布直方图中年龄在![]() 内的人数为
内的人数为![]() 人,对应的
人,对应的![]() 为
为![]() ,
,
所以补全的频率分布直方图如下:
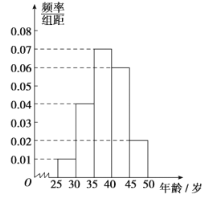
(2)由频数分布表知,在抽取的5人中,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,
,
记为![]() ,年龄在
,年龄在![]() 内的市民的人数为
内的市民的人数为![]() ,分别记为
,分别记为![]() ,
,![]() ,
,![]() ,
,![]() .
.
从这5人中任取2人的所有基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10种不同的取法.
,共10种不同的取法.
记“恰有1人的年龄在![]() 内”为事件
内”为事件![]() ,则
,则![]() 所包含的基本事件有4个:
所包含的基本事件有4个:![]() ,
,![]() ,
,![]() ,
,![]() ,共有4种不同的取法,
,共有4种不同的取法,
所以这2人中恰有1人的年龄在![]() 内的概率为
内的概率为![]() .
.

【题目】重庆市第八中学校为了解学生喜爱运动是否与性别有关,从全校学生中随机抽取50名学生进行问卷调查,得到如图所示的![]() 列联表.
列联表.
喜爱运动 | 不喜爱运动 | 合计 | |
男生 | 22 | 8 | 30 |
女生 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
附: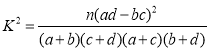 ,
,![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)能否有97.5%以上的把握认为“喜爱运动”与“性别”有关;
(2)用分层抽样的方法从被调查的20名女生中抽取5名进行问卷调查,求抽取喜爱运动的女生、不喜爱运动的女生各有多少的人;
(3)在(2)抽取的女生中,随机选出2人进行座谈,求至少有1名是喜爱运动的女生的概率.