题目内容
【题目】设函数![]() 是定义在
是定义在![]() 上的连续函数,且在
上的连续函数,且在![]() 处存在导数,若函数
处存在导数,若函数![]() 及其导函数
及其导函数![]() 满足
满足![]() ,则函数
,则函数![]() ( )
( )
A.既有极大值又有极小值B.有极大值 ,无极小值
C.有极小值,无极大值D.既无极大值也无极小值
【答案】C
【解析】
本题首先可以根据![]() 构造函数
构造函数![]() ,然后利用函数
,然后利用函数![]() 在
在![]() 处存在导数即可求出
处存在导数即可求出![]() 的值并求出函数
的值并求出函数![]() 的解析式,然后通过求导即可判断出函数
的解析式,然后通过求导即可判断出函数![]() 的极值。
的极值。
由题意可知,![]() ,即
,即![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
因为函数![]() 在
在![]() 处存在导数,所以
处存在导数,所以![]() 为定值,
为定值,![]() ,
,![]() ,
,
所以![]() ,
,
令![]() ,当
,当![]() 时,
时,![]() ,
,
构建函数![]() ,则有
,则有![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() ,
,![]() ,令
,令![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
因为![]() ,
,![]() ,
,
所以当![]() 时函数
时函数![]() 必有一解,
必有一解,
令这一解为![]() ,
,![]() ,则当
,则当![]() 时
时![]() ,
,
当![]() 时
时![]() ,
,
综上所述,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递增,
上单调递增,
所以![]() 有极小值,无极大值。
有极小值,无极大值。

练习册系列答案
相关题目
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,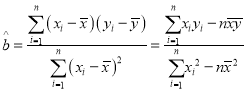 ,
,![]() 为数据平均数)
为数据平均数)


