题目内容

2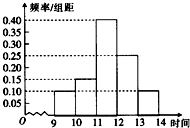．某商场在今年元霄节的促销活动中，对3月5日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为5万元，则11时至12时的销售额为（　　）
A．10万元B．15万元C．20万元D．25万元

分析 由频率分布直方图可得0.4÷0.1=4，也就是11时至12时的销售额为9时至10时的销售额的4倍，由此可得答案．

解答 解：由频率分布直方图可知9时至10时的$\frac{频率}{组距}$为0.10，11时至12时的$\frac{频率}{组距}$为0.40
∵0.4÷0.1=4，∴11时至12时的销售额为5×4=20
故选：C

点评 本题考查用样本估计总体，属基础题．

练习册系列答案
相关题目
8．已知数列{an}满足an+1=$\frac{1}{2-{a}_{n}}$（n∈N*），a1=0，记数列{an}的前n项和为Sn，cn=Sn-n+1+lnn．
（Ⅰ）令bn=$\frac{1}{1-{a}_{n}}$，求证数列{bn}为等差数列，并求其通项公式；
（Ⅱ）证明：（ i）对任意正整数n，|sin（bn•θ）|≤bn|sinθ|；
（ ii）数列{cn}从第2项开始是递增数列．
13．过点A（-2，3）作抛物线：y2=4x的两条切线l1，l2，设l1，l2与y轴分别交于点B，C，则△ABC的外接圆方程为（　　）
A．x2+y2-3x-2y+1=0B．x2+y2-2x-3y+1=0C．x2+y2-3x-4=0D．x2+y2+x-3y-2=0
10．在极坐标系中，圆C的方程为ρ=2$\sqrt{2}$sin（θ+$\frac{π}{4}$），以极点为坐标原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$（t为参数）．
（1）写出直线l的普通方程和圆C的直角坐方程；
（2）点P是圆C上任一点，求点P到直线l的距离的最大值．
17．如图所示的五个区域中，中心区域是一幅图画，现要求在其余四个区域中涂色，有四种颜色可供选择．要求每个区域只涂一种颜色，相邻区域所涂颜色不同，则不同的涂色方法种数为（　　）
A．84B．72C．64D．56
7．函数f（x）=log3（3+2x-x2）的定义域是{x|-1＜x＜3}．
14．某三棱锥的正视图和俯视图如图所示，则其左视图面积为（　　）
A．6B．$\frac{9}{2}$C．3D．$\frac{3}{2}$
11．已知函数f（x）=（x2-a）ex，a∈R．
（Ⅰ）当a=0时，求函数f（x）的单调区间；
（Ⅱ）若在区间（1，2）上存在不相等的实数m，n，使f（m）=f（n）成立，求a的取值范围；
（Ⅲ）若函数f（x）有两个不同的极值点x1，x2，求证：f（x1）f（x2）＜4e-2．
12．设实数x，y满足不等式组$\left\{\begin{array}{l}{x+y+1≥0}\\{x-2y+1≤0}\\{2x-y-1≤0}\end{array}\right.$，则z=2x-3y（　　）
A．有最大值-1，无最小值B．有最小值-1，无最大值
C．最小值-2，最大值3D．有最小值-2，无最大值

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网