题目内容
10.在极坐标系中,圆C的方程为ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),以极点为坐标原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$(t为参数).(1)写出直线l的普通方程和圆C的直角坐方程;
(2)点P是圆C上任一点,求点P到直线l的距离的最大值.
分析 (1)把t=x代入y=1+2t,可得直线l的普通方程;由圆C的方程为ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开化为:ρ2=2$\sqrt{2}×\frac{\sqrt{2}}{2}$(ρsinθ+ρcosθ),把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出;
(2)圆心C(1,1)到直线l的距离d,可得点P到直线l的距离的最大值=d+r.
解答 解:(1)直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=1+2t}\end{array}\right.$(t为参数),把t=x代入y=1+2t,可得y=2x+1;
由圆C的方程为ρ=2$\sqrt{2}$sin(θ+$\frac{π}{4}$),展开化为:ρ2=2$\sqrt{2}×\frac{\sqrt{2}}{2}$(ρsinθ+ρcosθ),化为x2+y2=2x+2y,即(x-1)2+(y-1)2=2.
(2)圆心C(1,1)到直线l的距离d=$\frac{|2-1+1|}{\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
∴点P到直线l的距离的最大值=d+r=$\frac{2\sqrt{5}}{5}$+$\sqrt{2}$.
点评 本题考查了极坐标方程化为直角坐标方程、直线参数方程、点到直线的距离公式、圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.在等差数列{an}中,已知a18=3(4-a2),则该数列的前11项和S11等于( )
| A. | 33 | B. | 44 | C. | 55 | D. | 66 |
2.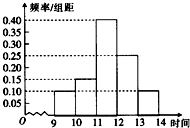 某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
 某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )| A. | 10万元 | B. | 15万元 | C. | 20万元 | D. | 25万元 |
 某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$.
某校对学生的上学时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,若用分层抽样的方法从该校400名学生中抽取一个容量为20的样本,设m,n表示某两名学生的上学所需时间,且已知m,n∈[40,60)∪[80,100],则事件|m-n|<20的概率为$\frac{2}{5}$. 如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.
如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.