题目内容
11.已知函数f(x)=(x2-a)ex,a∈R.(Ⅰ)当a=0时,求函数f(x)的单调区间;
(Ⅱ)若在区间(1,2)上存在不相等的实数m,n,使f(m)=f(n)成立,求a的取值范围;
(Ⅲ)若函数f(x)有两个不同的极值点x1,x2,求证:f(x1)f(x2)<4e-2.
分析 (Ⅰ)将a=0代入函数的表达式,求出函数的导数,解关于导函数的不等式,从而求出函数的单调区间;
(Ⅱ)问题转化为求使函数f(x)=ex(x2-a)在(1,2)上不为单调函数的a的取值范围,通过讨论x的范围,得到函数的单调性,进而求出a的范围;
(Ⅲ)先求出函数的导数,找到函数的极值点,从而证明出结论.
解答 解:(Ⅰ)当a=0时,f(x)=x2ex,f′(x)=ex(x2+2x),
由ex(2x2+2x)=0,解得:x=0,x=-2,
当x∈(-∞,-2)时,f′(x)>0,f(x)单调递增;
当x∈(-2,0)时,f′(x)<0,f(x)单调递减;
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增.
所以f(x)的单调增区间为(-∞,-2),(0,+∞),单调减区间为(-2,0);
(Ⅱ)依题意即求使函数f(x)=ex(x2-a)在(1,2)上不为单调函数的a的取值范围,
而f′(x)=ex(x2+2x-a),设g(x)=x2+2x-a,则g(1)=3-a,g(2)=8-a,
因为g(x)在(1,2)上为增函数.
当$\left\{\begin{array}{l}{g(1)=3-a<0}\\{g(2)=8-a>0}\end{array}\right.$,即当3<a<8时,函数g(x)在(1,2)上有且只有一个零点,设为x0,
当x∈(1,x0)时,g(x)<0,即f′(x)<0,f(x)为减函数;
当x∈(x0,2)时,g(x)>0,即f′(x)>0,f(x)为增函数,满足在(1,2)上不为单调函数.
当a≤3时,g(1)≥0,g(2)≥0,所以在(1,2)上g(x)>0成立(因g(x)在(1,2)上为增函数),
所以在(1,2)上f′(x)>0成立,即f(x)在(1,2)上为增函数,不合题意.
同理a≥8时,可判断f(x)在(1,2)为减函数,不合题意.
综上:3<a<8.
(Ⅲ)f′(x)=ex(x2+2x-a).
因为函数f(x)有两个不同的零点,即f′(x)有两个不同的零点,
即方程x2+2x-a=0的判别式△=4+4a>0,解得:a>-1,
由x2+2x-a=0,解得x1=-1-$\sqrt{a+1}$,x2=-1+$\sqrt{a+1}$.
此时x1+x2=-2,x1•x2=-a,
随着x变化,f(x)和f′(x)的变化情况如下:
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
∴f(x1)f(x2)=${e}^{{x}_{1}}$(${{x}_{1}}^{2}$-a)•${e}^{{x}_{2}}$(${{x}_{2}}^{2}$-a)
=${e}^{{x}_{1}{+x}_{2}}$${{{{[x}_{1}}^{2}x}_{2}}^{2}-a{{(x}_{1}}^{2}{{+x}_{2}}^{2}){+a}^{2}]$
=e-2[a2-a(4+2a)+a2]
=-4ae-2,
因为a>-1,所以-4ae-2<4e-2,
所以f(x1)f(x2)<4e-2.
点评 本题考查了函数的单调性,函数的极值问题,导数的应用,考查转化思想,分类讨论思想,熟练掌握基础知识并对其灵活应用是解题的关键,本题是一道难题.

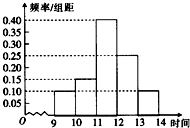 某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )
某商场在今年元霄节的促销活动中,对3月5日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为5万元,则11时至12时的销售额为( )| A. | 10万元 | B. | 15万元 | C. | 20万元 | D. | 25万元 |
 如图,将一张边长为1的正方形纸ABCD折叠,使得点B始终落在边AD上,则折起部分面积的最小值为( )
如图,将一张边长为1的正方形纸ABCD折叠,使得点B始终落在边AD上,则折起部分面积的最小值为( )| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |

| A. | -1008×2015 | B. | 1008×2015 | C. | -1008×2017 | D. | 1008×2017 |
 如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$.
如图所示,△ABC内接于⊙O,PA是⊙O的切线,PB⊥PA,BE=PE=2PD=4,则PA=4,AC=5$\sqrt{2}$. 已知一个空间几何体的所有棱长均为1cm,其表面展开图如图所示,则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3.
已知一个空间几何体的所有棱长均为1cm,其表面展开图如图所示,则该空间几何体的体积V=$1+\frac{{\sqrt{2}}}{6}$cm3.