题目内容
设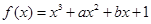 的导数
的导数 满足
满足 ,其中
,其中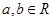 .
. 求曲线
求曲线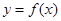 在点
在点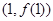 处的切线方程;
处的切线方程; 设
设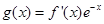 ,求函数
,求函数 的极值.
的极值.
(I)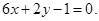
(II)函数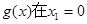 处取得极小值
处取得极小值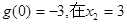 处取得极大值
处取得极大值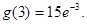
解析试题分析:(I)因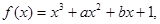 故
故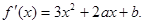
令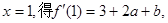 由已知
由已知
又令 由已知
由已知 因此
因此 解得
解得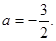 因此
因此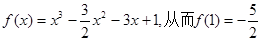
又因为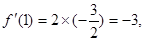 故曲线
故曲线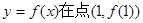 处的切线方程为
处的切线方程为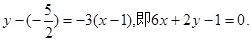
(II)由(I)知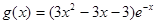 ,从而有
,从而有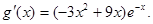
令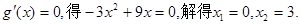
当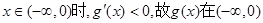 上为减函数;
上为减函数;
当 在(0,3)上为增函数;
在(0,3)上为增函数;
当 时,
时,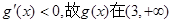 上为减函数;
上为减函数;
从而函数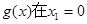 处取得极小值
处取得极小值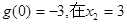 处取得极大值
处取得极大值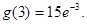
考点:导数的几何意义,利用导数研究函数的极值。
点评:典型题,在给定区间,导数非负,函数为增函数,导数非正,函数为减函数。求函数的极值问题,基本步骤是“求导数、求驻点、研究单调性、求极值”。

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 .
.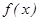 的单调区间;
的单调区间; 的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t
的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t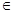 [1,2],函数
[1,2],函数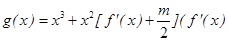 是
是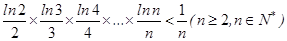
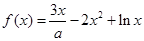
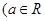 且
且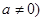 .
.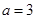 时,求在点
时,求在点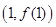 处的切线方程;
处的切线方程; 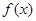 在区间
在区间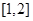 上为单调函数,求
上为单调函数,求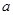 的取值范围.
的取值范围.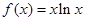
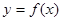 的图像在
的图像在 处的切线方程;
处的切线方程; ,求函数
,求函数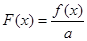 在
在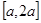 上的最小值.
上的最小值.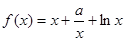 ,
, 时,求函数
时,求函数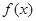 的单调增区间;
的单调增区间;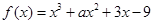 在
在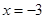 处取得极值
处取得极值 值
值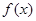 的单调递增区间.
的单调递增区间.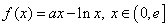 ,其中
,其中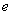 是自然常数,
是自然常数,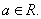
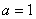 时,
时,  的单调性、极值;
的单调性、极值; ,使
,使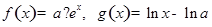 ,其中
,其中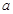 为常数,且函数
为常数,且函数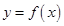 和
和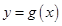 的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。
的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。