题目内容
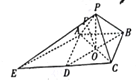
【题目】已知正方形![]() 的边长为2,分别以
的边长为2,分别以![]() ,
, ![]() 为一边在空间中作正三角形
为一边在空间中作正三角形![]() ,
, ![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)1.
【解析】试题分析:(1)证线面垂直,先证线线垂直,做出辅助线,根据长度关系,首先证得![]() ,再证得
,再证得![]() ,
, ![]() ,根据线面垂直的判定定理得到线面垂直;(2)根据条件可得到
,根据线面垂直的判定定理得到线面垂直;(2)根据条件可得到![]() 平面
平面![]() ,进而点
,进而点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 点到平面
点到平面![]() 的距离,取
的距离,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() 平面
平面![]() ,
, ![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
解析:
(1)连接![]() 交
交![]() 于点
于点![]() ,并连接
,并连接![]() ,则
,则![]() ,又∵
,又∵![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
即![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)由题知, ![]() ,且
,且![]() ,可得四边形
,可得四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∵点
,∵点![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 点到平面
点到平面![]() 的距离,取
的距离,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则由(1)可得
,则由(1)可得![]() .
.
在![]() 中,
中, ![]() ,则
,则![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
在![]() 中,
中, ![]() ,得点
,得点![]() 到平面
到平面![]() 的距离为1.
的距离为1.

【题目】某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:
打算观看 | 不打算观看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中数据b,c;
(2)判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关;
(3)为了计算“从10人中选出9人参加比赛”的情况有多少种,我们可以发现它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题:在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三(5)班,从中推选5人接受校园电视台采访,请根据上述方法,求被推选出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
【题目】深受广大球迷喜爱的某支欧洲足球队.在对球员的使用上总是进行数据分析,为了考察甲球员对球队的贡献,现作如下数据统计:
球队胜 | 球队负 | 总计 | |
甲参加 | 22 | b | 30 |
甲未参加 | c | 12 | d |
总计 | 30 | e | n |
(1)求b,c,d,e,n的值,据此能否有97.7%的把握认为球队胜利与甲球员参赛有关;
(2)根据以往的数据统计,乙球员能够胜任前锋、中锋、后卫以及守门员四个位置,且出场率分别为:0.2,0.5,0.2,0.1,当出任前锋、中锋、后卫以及守门员时,球队输球的概率依次为:0.4,0.2,0.6,0.2.则:
当他参加比赛时,求球队某场比赛输球的概率;
当他参加比赛时,在球队输了某场比赛的条件下,求乙球员担当前锋的概率;
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 7.879 | 10.828 |
![]() .
.
【题目】某印刷厂为了研究单册书籍的成本![]() (单位:元)与印刷册数
(单位:元)与印刷册数![]() (单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
(单位:千册)之间的关系,在印制某种书籍时进行了统计,相关数据见下表:
印刷册数 |
|
|
|
|
|
单册成本 |
|
|
|
|
|
根据以上数据,技术人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)为了评价两种模型的拟合效果,完成以下任务.
①完成下表(计算结果精确到![]() );
);
印刷册数 |
|
|
|
|
| |
单册成本 |
|
|
|
|
| |
模型甲 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
模型乙 | 估计值 |
|
|
| ||
残差 |
|
|
| |||
②分别计算模型甲与模型乙的残差平方和,并通过比较,判断哪个模型拟合效果更好.
(2)该书上市之后,受到广大读者热烈欢迎,不久便全部售罄,于是印刷厂决定进行二次印刷,根据市场调查,新需求量为![]() 千册,若印刷厂以每册
千册,若印刷厂以每册![]() 元的价格将书籍出售给订货商,求印刷厂二次印刷
元的价格将书籍出售给订货商,求印刷厂二次印刷![]() 千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
千册获得的利润?(按(1)中拟合效果较好的模型计算印刷单册书的成本).
【题目】随着互联网的迅速发展,越来越多的消费者开始选择网络购物这种消费方式某营销部门统计了2019年某月锦州的十大特产的网络销售情况得到网民对不同特产的最满意度![]() 和对应的销售额
和对应的销售额![]() (万元)数据,如下表:
(万元)数据,如下表:
特产种类 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最满意度 |
|
|
|
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
|
|
|
![]() 求销量额
求销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() ;
;
![]() 我们约定:销量额
我们约定:销量额![]() 关于最满意度
关于最满意度![]() 的相关系数
的相关系数![]() 的绝对值在
的绝对值在![]() 以上(含
以上(含![]() )是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额
)是线性相关性较强;否则,线性相关性较弱.如果没有达到较强线性相关,则采取“末位淘汰”制(即销售额最少的特产退出销售),并求在剔除“末位淘汰”的特产后的销量额![]() 关于最满意度
关于最满意度![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() ).
).
参考数据:![]()
![]() ,
,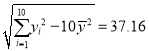 ,
,![]() ,
,![]() .
.
附:对于一组数据![]() .其回归直线方程
.其回归直线方程![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: ,
,![]() .线性相关系数
.线性相关系数

