题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
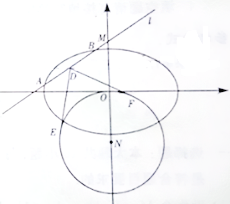
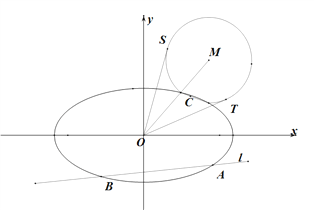
(Ⅱ)如图,动直线![]() :
: ![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点, ![]() 是椭圆
是椭圆![]() 上一点,直线
上一点,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() ,
, ![]() 是线段
是线段![]() 延长线上一点,且
延长线上一点,且![]() ,
, ![]() 的半径为
的半径为![]() ,
, ![]() 是
是![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .求
.求![]() 的最大值,并求取得最大值时直线
的最大值,并求取得最大值时直线![]() 的斜率.
的斜率.
【答案】(1)![]() (2)
(2)![]() 的最大值为
的最大值为![]() ,取得最大值时直线
,取得最大值时直线![]() 的斜率为
的斜率为![]() .
.
【解析】试题分析:(I)本小题由![]() ,
, ![]() 确定
确定![]() 即得.
即得.
(Ⅱ)通过联立方程组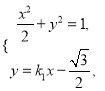 化简得到一元二次方程后应用韦达定理,应用弦长公式确定
化简得到一元二次方程后应用韦达定理,应用弦长公式确定![]() 及
及
圆![]() 的半径
的半径![]() 表达式.
表达式.
进一步求得直线![]() 的方程并与椭圆方程联立,确定得到
的方程并与椭圆方程联立,确定得到![]() 的表达式,研究其取值范围.这个过程中,可考虑利用换元思想,应用二次函数的性质及基本不等式.
的表达式,研究其取值范围.这个过程中,可考虑利用换元思想,应用二次函数的性质及基本不等式.
试题解析:(I)由题意知 ![]() ,
, ![]() ,
,
所以 ![]() ,
,
因此 椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,
联立方程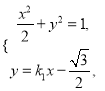
得![]() ,
,
由题意知![]() ,
,
且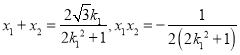 ,
,
所以 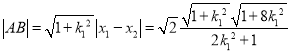 .
.
由题意可知圆![]() 的半径
的半径![]() 为
为
由题设知![]() ,
,
所以![]()
因此直线![]() 的方程为
的方程为![]() .
.
联立方程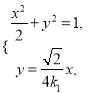
得![]() ,
,
因此 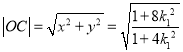 .
.
由题意可知 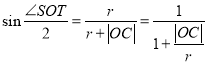 ,
,
而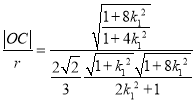
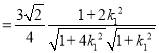 ,
,
令![]() ,
,
则![]() ,
,
因此 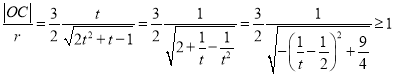 ,
,
当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时![]() ,
,
所以 ![]() ,
,
因此![]() ,
,
所以 ![]() 最大值为
最大值为![]() .
.
综上所述: ![]() 的最大值为
的最大值为![]() ,取得最大值时直线
,取得最大值时直线![]() 的斜率为
的斜率为![]() .
.

【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
【题目】2016年10月,继微信支付对提现转账收费后,支付宝也开始对提现转账收费,随着这两大目前用户使用粘度最高的第三方支付开始收费,业内人士分析,部分对价格敏感的用户或将回流至传统银行体系,某调查机构对此进行调查,并从参与调查的数万名支付宝用户中随机选取200人,把这200人分为3类:认为使用支付宝方便,仍使用支付宝提现转账的用户称为“![]() 类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“
类用户”;根据提现转账的多少确定是否使用支付宝的用户称为“![]() 类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“
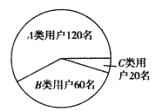
类用户”;提前将支付宝账户内的资金全部提现,以后转账全部通过银行的用户称为“![]() 类用户”,各类用户的人数如图所示:
类用户”,各类用户的人数如图所示:
同时把这200人按年龄分为青年人组与中老年人组,制成如图所示的![]() 列联表:
列联表:
| 非 | 合计 | |
青年 | 20 | ||
中老年 | 40 | ||
合计 | 200 |
(Ⅰ)完成![]() 列联表并判断是否有99.5%的把握认为“
列联表并判断是否有99.5%的把握认为“![]() 类用户与年龄有关”;
类用户与年龄有关”;
(Ⅱ)从这200人中按![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中
类用户进行分层抽样,从中抽取10人,再从这10人中随机抽取4人,求在这4人中![]() 类用户、
类用户、![]() 类用户、
类用户、![]() 类用户均存在的概率;
类用户均存在的概率;
(Ⅲ)把频率作为概率,从支付宝所有用户(人数很多)中随机抽取3人,用![]() 表示所选3人中
表示所选3人中![]() 类用户的人数,求
类用户的人数,求![]() 的分布列与期望.
的分布列与期望.
附:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)