题目内容
【题目】以下四个关于圆锥曲线命题:
①“曲线![]() 为椭圆”的充分不必要条件是“
为椭圆”的充分不必要条件是“![]() ”;
”;
②若双曲线的离心率![]() ,且与椭圆
,且与椭圆![]() 有相同的焦点,则该双曲线的渐近线方程为
有相同的焦点,则该双曲线的渐近线方程为![]() ;
;
③抛物线![]() 的准线方程为
的准线方程为![]() ;
;
④长为6的线段![]() 的端点
的端点![]() 分别在
分别在![]() 、
、![]() 轴上移动,动点
轴上移动,动点![]() 满足
满足![]() ,则动点
,则动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
其中正确命题的序号为_________.
【答案】③④
【解析】
对于①, 求出“曲线![]() 为椭圆”的充要条件,判断与“
为椭圆”的充要条件,判断与“![]() ”关系,即得①的正误;对于②,根据已知条件求出双曲线的方程,从而求出渐近线方程,即得②的正误;对于③,把抛物线的方程化为标准式,求出准线方程,即得③的正误;对于④,设
”关系,即得①的正误;对于②,根据已知条件求出双曲线的方程,从而求出渐近线方程,即得②的正误;对于③,把抛物线的方程化为标准式,求出准线方程,即得③的正误;对于④,设![]() ,根据
,根据![]() ,可得
,可得![]() ,代入
,代入![]() ,求出动点
,求出动点![]() 的轨迹方程,即得④的正误.
的轨迹方程,即得④的正误.
对于①, “曲线![]() 为椭圆”的充要条件是“
为椭圆”的充要条件是“![]() 且
且![]() ”.
”.
所以“曲线![]() 为椭圆”的必要不充分条件是“
为椭圆”的必要不充分条件是“![]() ”,故①错误;
”,故①错误;
对于②,椭圆![]() 的焦点为
的焦点为![]() ,又双曲线的离心率
,又双曲线的离心率![]() ,所以双曲线的方程为
,所以双曲线的方程为![]() ,所以双曲线的渐近线方程为
,所以双曲线的渐近线方程为![]() ,故②错误;
,故②错误;
对于③,抛物线![]() 的方程化为标准式
的方程化为标准式![]() ,准线方程为
,准线方程为![]() ,故③正确;
,故③正确;
对于④,设![]() ,
,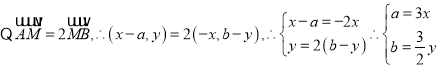 ,
,
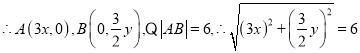 ,即
,即![]() ,即动点
,即动点![]() 的轨迹方程为
的轨迹方程为![]() .故④正确.
.故④正确.
故答案为:③④.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|