题目内容
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(1)设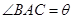 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为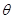 的函数
的函数 ;
;
(2)试确定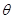 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.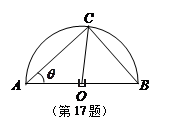
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧
 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)(1)设
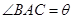 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为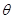 的函数
的函数 ;
;(2)试确定
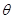 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.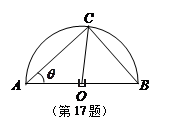
(1)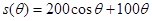 ,
,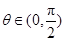 ,(2)当
,(2)当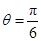 时,绿化带总长度最大.
时,绿化带总长度最大.
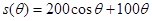 ,
,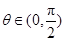 ,(2)当
,(2)当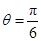 时,绿化带总长度最大.
时,绿化带总长度最大.试题分析:(1)解实际问题应用题,关键正确理解题意,正确列出等量关系或函数关系式.本题要注意着重号. 绿化带总长度
 等于2AC与弧长BC之和. 在直角三角形
等于2AC与弧长BC之和. 在直角三角形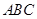 中,
中,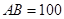 ,
,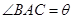 ,所以
,所以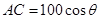 .由于
.由于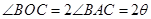 ,所以弧
,所以弧 的长为
的长为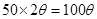 .所以
.所以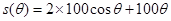 ,作为函数解析式,必须明确其定义域,
,作为函数解析式,必须明确其定义域,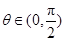 .(2)利用导数求
.(2)利用导数求 最大值. 令
最大值. 令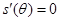 ,则
,则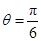 ,列表分析可知当
,列表分析可知当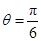 时,
时, 取极大值,即为最大值.
取极大值,即为最大值.【解】(1)如图,连接
 ,设圆心为
,设圆心为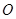 ,连接
,连接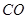 .
.在直角三角形
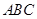 中,
中,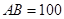 ,
,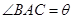 ,
,所以
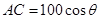 .
.由于
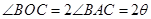 ,所以弧
,所以弧 的长为
的长为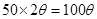 . 3分
. 3分所以
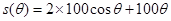 ,
,即
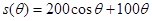 ,
,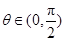 . 7分
. 7分(2)
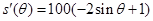 , 9分
, 9分令
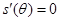 ,则
,则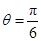 , 11分
, 11分列表如下:
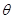 | 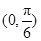 | 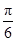 | 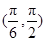 |
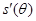 | + | 0 | 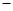 |
 |  | 极大值 |  |
所以,当
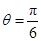 时,
时, 取极大值,即为最大值. 13分
取极大值,即为最大值. 13分答:当
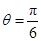 时,绿化带总长度最大. 14分
时,绿化带总长度最大. 14分
练习册系列答案
相关题目
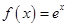 .
.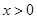 时,设
时,设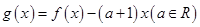 .讨论函数
.讨论函数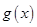 的单调性;
的单调性;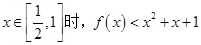 .
. ,其导函数
,其导函数 的图象经过点
的图象经过点 ,
, ,如图所示.
,如图所示. 的极大值点;
的极大值点; 的值;
的值; ,求
,求 上的最小值.
上的最小值.
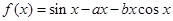
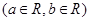 .
.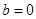 ,讨论函数
,讨论函数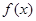 在区间
在区间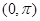 上的单调性;
上的单调性;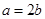 且对任意的
且对任意的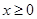 ,都有
,都有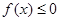 恒成立,求实数
恒成立,求实数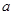 的取值范围.
的取值范围.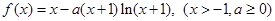 .
.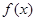 的单调区间;
的单调区间;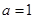 时,若方程
时,若方程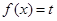 在
在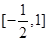 上有两个实数解,求实数
上有两个实数解,求实数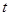 的取值范围;
的取值范围;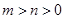 时,
时,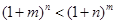 .
.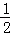 x2﹣lnx的单调递减区间为( )
x2﹣lnx的单调递减区间为( ) 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是
的取值范围是 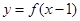 的图象关于点(1,0)对称,且当
的图象关于点(1,0)对称,且当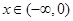 时,
时, 成立(其中
成立(其中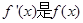 的导函数),若
的导函数),若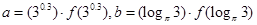 ,
,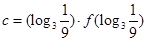 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )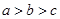
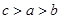
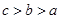
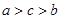
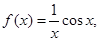 则
则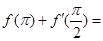 ( )
( )