题目内容
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 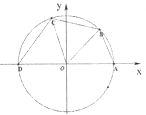
(1)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(2)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
【答案】
(1)解:∵B( ![]() ,
, ![]() ),
),
∴cos∠AOB= ![]() ,sin∠AOB=
,sin∠AOB= ![]() ;
;
∴cos∠AOC=cos(∠AOB+∠BOC)
=cos∠AOBcos∠BOC﹣sin∠AOBsin∠BOC
= ![]() ×
× ![]() ﹣
﹣ ![]() ×
× ![]()
= ![]() ;
;
(2)解:等腰三角形AOB中,求得|AB|=2|OB|sin ![]() =2sin
=2sin ![]() ,
,
等腰三角形COD中,求得
|CD|=2|OC|sin ![]() =2sin(
=2sin( ![]() ﹣
﹣ ![]() );
);
∴y=|AB|+|BC|+|CD|+|DA|
=3+2sin ![]() +2sin(
+2sin( ![]() ﹣
﹣ ![]() )
)
=3+2sin( ![]() +
+ ![]() );
);
由0<x< ![]() 得,当
得,当 ![]() +
+ ![]() =
= ![]() ,
,
即x= ![]() 时,y取得最大值5
时,y取得最大值5
【解析】(1)由三角函数的定义,写出cos∠AOB与sin∠AOB的值,再计算cos∠AOC的值;(2)根据等腰三角形的知识,求出|AB|、|CD|的值,再写出函数y的解析式,求出y的最大值即可.

练习册系列答案
相关题目