题目内容
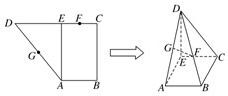 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+| 3 |
(1)求证:BC⊥平面CDE;
(2)求证:FG∥平面BCD;
(3)求四棱锥D-ABCE的体积.
分析:(1)由已知BC⊥CE,只需再证明BC垂直于与CE相交的一条直线即可,而根据条件容易证明DE⊥平面ABCE.从而可以证明BC⊥DE,而CE∩DE=E,所以可以证明BC⊥平面DCE.
(2)需要构造一个GF所在的平面,使得该平面与平面BCD;使用线面平行的定义或者面面平行的性质证明即可;
(3)由于在解决第一问的时已经证明了DE⊥平面ABCE,因此DE即为该四棱锥的高,求出底面ABCE的面积,代入椎体体积公式求即可.
(2)需要构造一个GF所在的平面,使得该平面与平面BCD;使用线面平行的定义或者面面平行的性质证明即可;
(3)由于在解决第一问的时已经证明了DE⊥平面ABCE,因此DE即为该四棱锥的高,求出底面ABCE的面积,代入椎体体积公式求即可.
解答: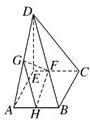 解:(1)证明:由已知得:
解:(1)证明:由已知得:
DE⊥AE,DE⊥EC,∴DE⊥平面ABCE.
∴DE⊥BC.又BC⊥CE,CE∩DE=E,
∴BC⊥平面DCE.
(2)证明:取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥平面BCD,FH∥平面BCD.
又GH∩FH=H,
∴平面FHG∥平面BCD,
∴FG∥平面BCD(由线线平行证明亦可).
(3)V=
×1×2×
=
.
 解:(1)证明:由已知得:
解:(1)证明:由已知得:DE⊥AE,DE⊥EC,∴DE⊥平面ABCE.
∴DE⊥BC.又BC⊥CE,CE∩DE=E,
∴BC⊥平面DCE.
(2)证明:取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥平面BCD,FH∥平面BCD.
又GH∩FH=H,
∴平面FHG∥平面BCD,
∴FG∥平面BCD(由线线平行证明亦可).
(3)V=
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
点评:本题考查直线与平面的位置关系中的平行与垂直的证明,以及椎体体积的求法,在证明时要注意线线垂直与线面垂直的转化,线面平行与面面平行的转化,体现灵活的转化思想.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
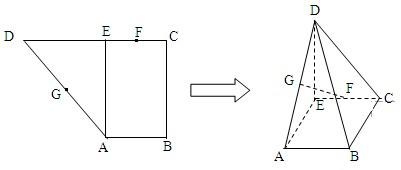
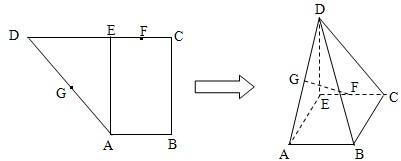
 已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足
已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=