题目内容
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+| 3 |
(1)求证:BC⊥面CDE;
(2)求证:FG∥面BCD.
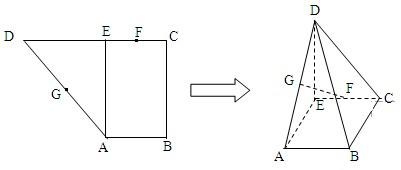
分析:(1)欲证BC⊥面DCE,根据直线与平面垂直的判定定理可知只需证BC与面DCE内两相交直线垂直,而DE⊥BC,BC⊥CE,满足定理的条件;
(2)取AB中点H,连接GH,FH,欲证GF∥面BCD,可证面FHG∥面BCD,根据GH∥面BCD,FH∥面BCD满足面面平行的性质定理.
(2)取AB中点H,连接GH,FH,欲证GF∥面BCD,可证面FHG∥面BCD,根据GH∥面BCD,FH∥面BCD满足面面平行的性质定理.
解答:证明:(1)由已知得:DE⊥AE,DE⊥EC,
∴DE⊥面ABCE∴DE⊥BC,又BC⊥CE,∴BC⊥面DCE;
(2)取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD
∴面FHG∥面BCD,
∴GF∥面BCD
∴DE⊥面ABCE∴DE⊥BC,又BC⊥CE,∴BC⊥面DCE;
(2)取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD
∴面FHG∥面BCD,
∴GF∥面BCD
点评:本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
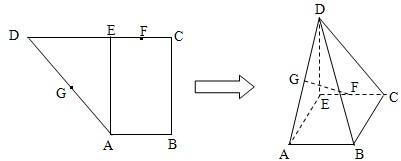
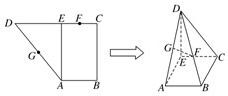 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ 已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足
已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=