题目内容
 已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足AE=
已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足AE=| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
(1)求证:AE⊥平面ABCD;
(2)求二面角D-CE-A的大小.
分析:(1)欲证AE⊥平面ABCD,根据直线与平面垂直的判定定理可知只需证AE与平面ABCD内两相交直线垂直,而EA⊥AD,EA⊥AB,AB∩AD=A,满足定理条件
(2)由图,可以A为原点,建立空间直角坐标系,写出各点的坐标,由向量运算求出两个平面的法向量,再由数量积公式求出两个平面的夹角的余弦值.
(2)由图,可以A为原点,建立空间直角坐标系,写出各点的坐标,由向量运算求出两个平面的法向量,再由数量积公式求出两个平面的夹角的余弦值.
解答:解:(1)折叠后由已知:AE=
AD=1,DE=2,AD=
,∴AE2+AD2=DE2,即:AE⊥AD,又AE⊥AB,AD∩AB=A,∴AE⊥平面ABCD
(2)(Ⅱ)解:以点A为坐标原点,建立如图空间直角坐标系,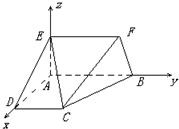
则A(0,0,0),C(
,1,0),E(0,0,1),D(
, 0,0),
=(0,1,0),
=(-
,0,1)
设平面DCE的一个法向量为
=(x,y,z),则
取x=1则得出
=(1,0,
)
设平面CEA的一个法向量为
=(x′,y′,z′)
=(
, 1,0),
=(0,0,1)
取x=1,则得
=(1,-
,0)
故cos<
,
>=
=
=
,
所以二面角D-CE-A的大小arccos
.
| 1 |
| 3 |
| 3 |
(2)(Ⅱ)解:以点A为坐标原点,建立如图空间直角坐标系,

则A(0,0,0),C(
| 3 |
| 3 |
| DC |
| DE |
| 3 |
设平面DCE的一个法向量为
| m |
|
取x=1则得出
| m |
| 3 |
设平面CEA的一个法向量为
| n |
| AC |
| 3 |
| AE |
|
取x=1,则得
| n |
| 3 |
故cos<
| m |
| n |
| ||||
|
|
| 1 |
| 2×2 |
| 1 |
| 4 |
所以二面角D-CE-A的大小arccos
| 1 |
| 4 |
点评:本题考查直线与平面垂直的判定,用空间向量求二面角的夹角.考查考查空间想象、推理论证、计算能力.利用向量求解决立体几何问题是近几年高考的热点,向量法解决立体几何问题降低了思维难度,化推理为计算,使得几何求解、证明变得简单,此法也有不足,需要建立坐标系,且运算量较大.

练习册系列答案
相关题目
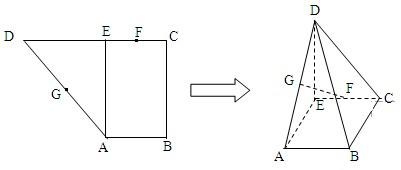
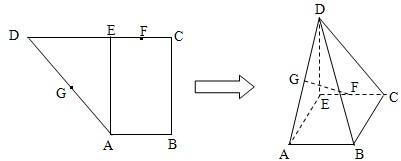
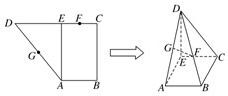 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=