题目内容
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+| 3 |
(1)求证:FG∥面BCD;
(2)设四棱锥D-ABCE的体积为V,其外接球体积为V′,求V:V′的值.
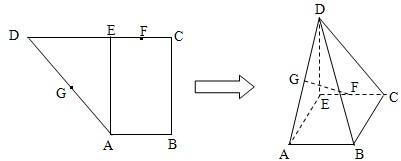
分析:(1)取AB中点H,连接GH,FH,利用三角形中位线定理,我们易判断GH∥BD,FH∥BC,进而根据面面平行的判定定理,得到面FHG∥面BCD,结合面面平等的性质,即可得到结论.
(2)由已知中AB⊥BC,AB=1,BC=2,CD=1+
,代入棱锥体积公式,易求出棱锥的体积,又E点三条棱互相垂直,故棱锥的外接球半径与以AE,CD,DE为棱长的长方体的外接球半径相等,求出外接球半径后,即可得到V:V′的值.
(2)由已知中AB⊥BC,AB=1,BC=2,CD=1+
| 3 |
解答:解:
(1)证明:取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD
∴面FHG∥面BCD,
∴GF∥面BCD(6分)
(2)V=
×2×1×
=
又外接球半径R=
=
∴V′=
π•2
=
π
∴V:V′=
(12分)
(1)证明:取AB中点H,连接GH,FH,
∴GH∥BD,FH∥BC,
∴GH∥面BCD,FH∥面BCD
∴面FHG∥面BCD,
∴GF∥面BCD(6分)
(2)V=
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
又外接球半径R=
| 1 |
| 2 |
12+22+(
|
| 2 |
∴V′=
| 4 |
| 3 |
| 2 |
8
| ||
| 3 |
∴V:V′=
| ||
| 8π |
点评:本题考查的知识点是直线与平面平等的判定及棱锥和球的体积,其中根据E点三条棱互相垂直,故棱锥的外接球半径与以AE,CD,DE为棱长的长方体的外接球半径相等,求出外接球半径是解答本题的关键点.

练习册系列答案
相关题目
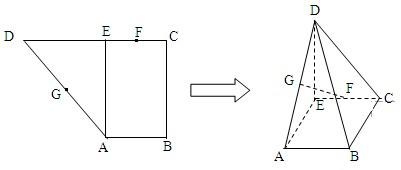
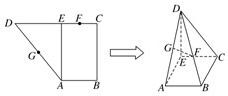 已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+
已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+ 已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足
已知直角梯形ABCD中,AB∥CD,∠BAD=90°,且AB=2,AD=3,CD=1,点E、F分别在AD、BC上,满足 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=