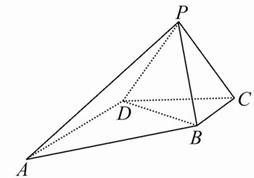
题目内容
 如图,已知直角梯形ABCD的上底BC=
如图,已知直角梯形ABCD的上底BC=| 2 |
| 1 |
| 2 |
(1)证明:AB⊥PB;
(2)求二面角P-AB-D的大小.
(3)求三棱锥A-PBD的体积.
分析:(1)由已知中中在直角梯形ABCD中,因为AD=2
,BC=
,CD=2,我们易求出AB值,双由为BC⊥CD,平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,则BC⊥平面PDC,再由勾定理得到,我们可得AB⊥PB;
(2)设线段DC的中点为E,连接PE,EB,结合△PCD是等边三角形,平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,我们易得AB⊥PE,AB⊥PB,则∠PBE就是二面角P-AB-D的平面角,解△PBE即可得到答案.
(3)VA-PBD=VP-ABD,求出棱锥的底面面积及高,代入棱锥体积公式即可得到答案.
| 2 |
| 2 |
(2)设线段DC的中点为E,连接PE,EB,结合△PCD是等边三角形,平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,我们易得AB⊥PE,AB⊥PB,则∠PBE就是二面角P-AB-D的平面角,解△PBE即可得到答案.
(3)VA-PBD=VP-ABD,求出棱锥的底面面积及高,代入棱锥体积公式即可得到答案.
解答: 证明:(1)在直角梯形ABCD中,因为AD=2
证明:(1)在直角梯形ABCD中,因为AD=2
,BC=
,CD=2
所以AB=
=
.
因为BC⊥CD,平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,所以BC⊥平面PDC,因此在Rt△BCP中,PB=
=
.
因为BC∥AD所以AD⊥平面PDC,所以在Rt△PAD中,
PA=
=
=
.
所以在△PAB中,PA2=AB2+PB2,所以AB⊥PB.
解:(2)设线段DC的中点为E,连接PE,EB
因为△PCD是等边三角形,所以PE⊥C,
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,所以PE⊥平面ABCD,因此AB⊥PE,由(1)知AB⊥PB,所以AB⊥平面PEB,所以AB⊥BE,因此∠PBE就是二面角P-AB-D的平面角,在Rt△PBE中,
sin∠PBE=
=
=
,所以∠PBE=
.
解:(3)∵VA-PBD=VP-ABD=
•S△ABD•PE=
×
•AD•DC•
=
×
×2
×2×
=
 证明:(1)在直角梯形ABCD中,因为AD=2
证明:(1)在直角梯形ABCD中,因为AD=2| 2 |
| 2 |
所以AB=
| (AD-BC)2+CD2 |
| 6 |
因为BC⊥CD,平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,所以BC⊥平面PDC,因此在Rt△BCP中,PB=
| BC2+PC2 |
| 6 |
因为BC∥AD所以AD⊥平面PDC,所以在Rt△PAD中,
PA=
| AD2+PD2 |
(2
|
| 12 |
所以在△PAB中,PA2=AB2+PB2,所以AB⊥PB.
解:(2)设线段DC的中点为E,连接PE,EB
因为△PCD是等边三角形,所以PE⊥C,
因为平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,所以PE⊥平面ABCD,因此AB⊥PE,由(1)知AB⊥PB,所以AB⊥平面PEB,所以AB⊥BE,因此∠PBE就是二面角P-AB-D的平面角,在Rt△PBE中,
sin∠PBE=
| PE |
| PB |
| ||
|
| ||
| 2 |
| π |
| 4 |
解:(3)∵VA-PBD=VP-ABD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
2
| ||
| 3 |
点评:本题考查的知识点是直线与平面垂直的性质,棱锥的体积,二面角平面角的求法,在求二面角时,根据三垂线定理找到二面角的平面角是解答的关键.

练习册系列答案
相关题目
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.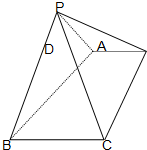 如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.
如图:已知四棱锥P-ABCD的底面为直角梯形,AD∥BC,∠BCD=90,PA=PB,PC=PD.