题目内容
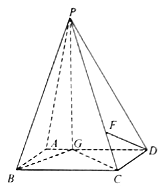
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,且
,且![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点,四面体
的中点,四面体![]() 的体积为
的体积为![]() .
.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)若![]() 点是棱
点是棱![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ) ![]()
【解析】
(Ⅰ)先利用等体积法求出![]() 的长,在平面
的长,在平面![]() 内, 过
内, 过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() (或其补角)就是异面直线
(或其补角)就是异面直线![]() 与
与![]() 所成的角,在
所成的角,在![]() 中利用余弦定理求出此角即可;(Ⅱ)在平面
中利用余弦定理求出此角即可;(Ⅱ)在平面![]() 内,过
内,过![]() 作
作![]() ,交
,交![]() 延长线于
延长线于![]() ,则
,则![]() 平面
平面![]() 推得
推得![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离,在
的距离,在![]() 利用边角关系求出
利用边角关系求出![]() 长; (Ⅲ)在平面
长; (Ⅲ)在平面![]() 内,过
内,过![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() ,先证明
,先证明![]() ,然后利用三角形相似对应边成比例建立等量关系即可.
,然后利用三角形相似对应边成比例建立等量关系即可.
(I)由已知![]() ,
,
∴![]() .
.
在平面![]() 内,过
内,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,则
,则![]() (或其补角)就是异面直线
(或其补角)就是异面直线![]() 与
与![]() 所成的角.
所成的角.

在![]() 中,
中,![]() ,
,
由余弦定理得, ![]() ,
,
∴异面直线![]() 与
与![]() 所成的角的余弦值为
所成的角的余弦值为![]() .
.
(II)∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ∴平面
∴平面![]() 平面
平面![]() ,
,
在平面![]() 内,过
内,过![]() 作
作![]() ,交
,交![]() 延长线于
延长线于![]() ,则
,则![]() 平面
平面![]() ∴
∴![]() 的长就是点
的长就是点![]() 到平面
到平面![]() 的距离.
的距离.
∵![]() .
.
在![]() ,
,![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
(III)在平面![]() 内,过
内,过![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() ,
,
又因为![]() ,
,![]()
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() .
.
由平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ∴
∴![]() ;
;
由![]() 得:
得: ![]() .
.
∵ ,∴由
,∴由![]() 可得
可得![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
组别 | 分组 | 频数 | 频率 |
第一组 |
| 10 | 0.1 |
第二组 |
| 20 | 0.2 |
第三组 |
| 40 | 0.4 |
第四组 |
| 25 | 0.25 |
第五组 |
| 5 | 0.05 |
合计 | 100 | 1 |
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?