题目内容
((本题14分)已知函数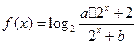 (
(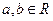 )的图象过点(1,2),它的反函数的图象也过点(1,2)。
)的图象过点(1,2),它的反函数的图象也过点(1,2)。
(1)求实数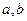 的值,并求函数
的值,并求函数 的定义域和值域;
的定义域和值域;
(2)判断函数 在其定义域上的单调性(不必证明),并解不等式
在其定义域上的单调性(不必证明),并解不等式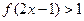 。
。
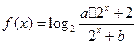 (
(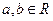 )的图象过点(1,2),它的反函数的图象也过点(1,2)。
)的图象过点(1,2),它的反函数的图象也过点(1,2)。(1)求实数
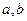 的值,并求函数
的值,并求函数 的定义域和值域;
的定义域和值域;(2)判断函数
 在其定义域上的单调性(不必证明),并解不等式
在其定义域上的单调性(不必证明),并解不等式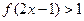 。
。解:(1)依题意,函数 过点(1,2)和(2,1),则……………1分
过点(1,2)和(2,1),则……………1分
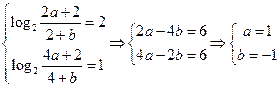 ……………3分
……………3分
所以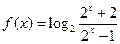 ……………4分
……………4分
由 ,
,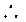
 的定义域为:
的定义域为: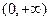 。……6分
。……6分
令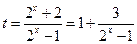 ,
,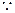
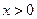
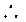
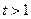 ,
,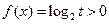
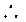
 的值域为:
的值域为: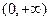 ………8分
………8分
(2)函数 在
在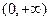 上为减函数。……………9分
上为减函数。……………9分
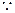 函数
函数 过点(2,1),
过点(2,1),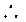
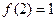 ,则
,则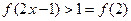
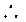
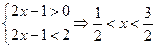 即不等式
即不等式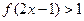 的解集为
的解集为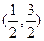 。…………14分
。…………14分
 过点(1,2)和(2,1),则……………1分
过点(1,2)和(2,1),则……………1分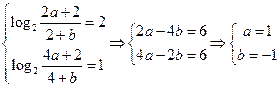 ……………3分
……………3分 所以
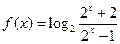 ……………4分
……………4分由
 ,
,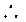
 的定义域为:
的定义域为: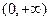 。……6分
。……6分令
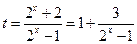 ,
,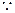
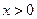
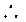
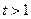 ,
,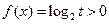
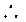
 的值域为:
的值域为: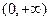 ………8分
………8分(2)函数
 在
在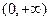 上为减函数。……………9分
上为减函数。……………9分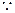 函数
函数 过点(2,1),
过点(2,1),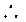
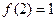 ,则
,则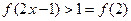
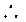
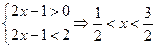 即不等式
即不等式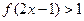 的解集为
的解集为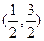 。…………14分
。…………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
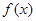 同时满足如下三个条件,求
同时满足如下三个条件,求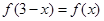 ;②
;②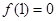 ;③对任意实数
;③对任意实数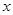 ,都有
,都有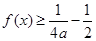 恒成立.
恒成立.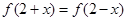 ,(2)被
,(2)被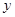 轴截距为6,求此函数解析式
轴截距为6,求此函数解析式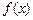 与产量
与产量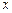 之间的关系式为
之间的关系式为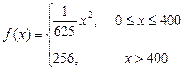 ,每件产品的售价
,每件产品的售价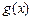 与产量
与产量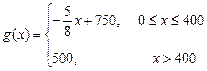 .
.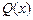 与产量
与产量 B
B 
 D
D 
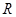 上的函数
上的函数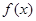 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表: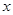
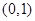 B、
B、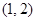 C、
C、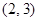 D、
D、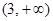
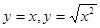
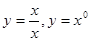
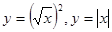
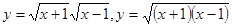
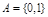 ,
,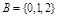 ,则从
,则从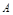 到
到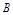 的映射有( )
的映射有( )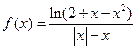 的定义域为
的定义域为 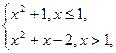 则
则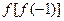 的值为______
的值为______