题目内容
3.△ABC为等腰直角三角形,OA=1,OC为斜边AB上的高,P为线段OC的中点,则$\overrightarrow{AP}•\overrightarrow{OP}$=$\frac{1}{4}$.分析 可分别以CB,CA两直线为x轴,y轴,建立平面直角坐标系,根据条件容易求出CA=CB=$\sqrt{2}$,从而可确定图形上各点的坐标,从而得出向量$\overrightarrow{AP},\overrightarrow{OP}$的坐标,然后进行数量积的坐标运算即可.
解答 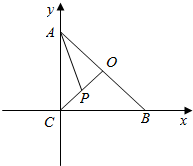 解:如图,分别以边CB,CA所在直线为x,y轴,建立如图所示平面直角坐标系;
解:如图,分别以边CB,CA所在直线为x,y轴,建立如图所示平面直角坐标系;
根据条件知CA=CB=$\sqrt{2}$;
∴A(0,$\sqrt{2}$),B($\sqrt{2}$,0),O($\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}$),P($\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4}$);
∴$\overrightarrow{AP}=(\frac{\sqrt{2}}{4},-\frac{3\sqrt{2}}{4}),\overrightarrow{OP}=(-\frac{\sqrt{2}}{4},-\frac{\sqrt{2}}{4})$;
∴$\overrightarrow{AP}•\overrightarrow{OP}=-\frac{1}{8}+\frac{3}{8}=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 考查建立平面直角坐标系,利用向量坐标解决向量问题的方法,建立完坐标系能够求出图形上点的坐标,从而求出向量的坐标,向量数量积的坐标运算.

练习册系列答案
相关题目
8.函数f(x)=$\frac{{{e^x}-{e^{-x}}}}{2}$是( )
| A. | 偶函数,在(0,+∞)是增函数 | B. | 奇函数,在(0,+∞)是增函数 | ||
| C. | 偶函数,在(0,+∞)是减函数 | D. | 奇函数,在(0,+∞)是减函数 |
12.已知集合A={x|x2-4x-5<0},B={x|2<x<4},则A∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |