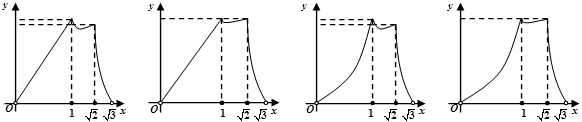题目内容
对于函数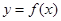 ,如果存在区间
,如果存在区间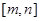 ,同时满足下列条件:①
,同时满足下列条件:① 在
在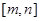 内是单调的;②当定义域是
内是单调的;②当定义域是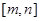 时,
时, 的值域也是
的值域也是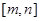 ,则称
,则称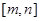 是该函数的“和谐区间”.若函数
是该函数的“和谐区间”.若函数 存在“和谐区间”,则
存在“和谐区间”,则 的取值范围是( )
的取值范围是( )
A.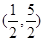 | B.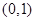 | C.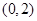 | D.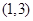 |
B
解析试题分析:由题意可得函数 在区间
在区间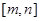 是单调的,
是单调的,
所以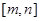 ⊆(﹣
⊆(﹣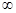 ,0)或
,0)或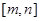 ⊆(0,+
⊆(0,+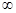 ),则f(m)=m,f(n)=n,
),则f(m)=m,f(n)=n,
故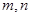 是方程
是方程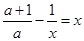 的两个同号的实数根,
的两个同号的实数根,
即方程 有两个同号的实数根,注意到
有两个同号的实数根,注意到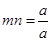 =1>0,
=1>0,
故只需△=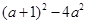 >0,解得
>0,解得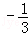
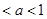 ,
,
结合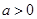 ,可得
,可得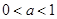 .
.
考点:1、函数单调性的判断与证明;2、函数的值域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数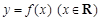 满足
满足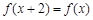 ,且
,且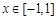 时,
时,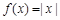 ,则函数
,则函数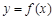 的图象与函数
的图象与函数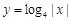 的图象的交点的个数为 ( )
的图象的交点的个数为 ( )
| A.3 | B.4 | C.6 | D.8 |
已知函数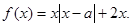 若存在
若存在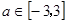 ,使得关于
,使得关于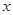 的方程
的方程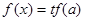 有三个不相等的实数根,则实数
有三个不相等的实数根,则实数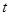 的取值范围是( )
的取值范围是( )
A. | B.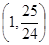 | C.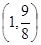 | D.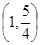 |
已知函数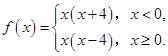 则函数
则函数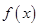 的零点个数为 ( )
的零点个数为 ( )
A. | B. | C. | D.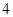 |
已知定义在R上的偶函数f(x)满足:?x∈R恒有f(x+2)=f(x)-f(1).且当x∈[2,3]时,f(x)=-2(x-3)2.若函数y=f(x)-loga(x+1)在(0,+∞)上至少有三个零点,则实数a的取值范围为( )
A.(0, ) ) | B.(0,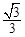 ) ) | C.(1,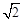 ) ) | D.(1,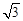 ) ) |
已知偶函数 满足
满足 ,且在区间
,且在区间 上单调递增.不等式
上单调递增.不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
 ,函数
,函数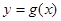 是它的反函数,则函数
是它的反函数,则函数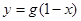 的大致图象是( )
的大致图象是( )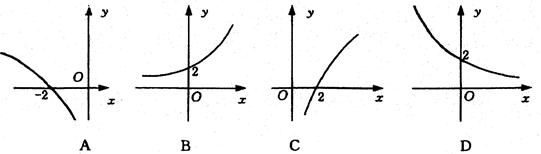
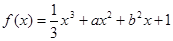 ,若
,若 是从
是从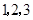 三个数中任取的一个数,
三个数中任取的一个数,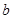 是从
是从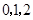 三个数中任取的一个数,则该函数有两个极值点的概率为( )
三个数中任取的一个数,则该函数有两个极值点的概率为( )
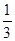
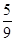
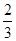
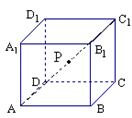
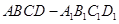 的对角线
的对角线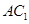 上任取一点P,以
上任取一点P,以 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设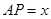 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数