题目内容
【题目】在数列
中，
.
（1）判断数列
是否为等比数列？并说明理由；
（2）若对任意正整数
，
恒成立，求首项
的取值范围.
【答案】（1）答案见解析.（2）
【解析】
（1）转化条件得
，由等比数列的概念即可得解；
（2）易得当
时，符合条件；当
时，
，根据
为奇数、为偶数分类讨论，由恒成立问题的解决办法即可得解.
（1）因为
，所以
，
所以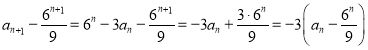
，
所以
，
所以当
即时，
，
所以当时，数列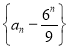
不是等比数列；
当
，即时，
，所以
，
所以当时，数列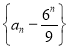是等比数列；
（2）由（1）知，当时，
，所以
恒成立；
当时，数列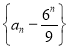是等比数列，且首项为
，公比为
，
所以
，
即.
当为奇数时，
，所以
.
又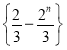
单调递减，所以
时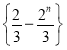，取得最大值，所以
；
当为偶数时，，所以
.
又
单调递增，所以当
时，的最小值为2，所以
，
所以
；
综上，首项
的取值范围为.
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
【题目】某网站针对“2016年春节放假安排”开展网上问卷调查，提出了A，B两种放假方案，调查结果如表：(单位：万人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知从所有参与调查的人中任选1人是“老年人”的概率为
.
(1)求n的值；
(2)从参与调查的“老年人”中，用分层抽样的方法抽取6人，在这6人中任意选取2人，求恰好有1人“支持B方案”的概率．
【题目】绵阳是党中央、国务院批准建设的中国唯一的科技城，重要的国防科研和电子工业生产基地，市某科研单位在研发过程中发现了一种新合金材料，由大数据测得该产品的性能指标值
（值越大产品的性能越好）与这种新合金材料的含量
（单位：克）的关系为：当
时，是的二次函数；当
时，
测得部分数据如表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求关于的函数关系式
；
（2）求该新合金材料的含量为何值时产品的性能达到最佳．
