题目内容
【题目】如图,四边形 ![]() 为菱形,四边形
为菱形,四边形 ![]() 为平行四边形,设
为平行四边形,设 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,
, ![]() .
.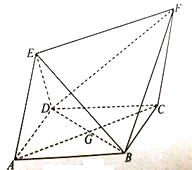
(1)证明:平面 ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,求三棱锥
,求三棱锥 ![]() 的体积.
的体积.
【答案】
(1)
解:证明:连接 ![]() ,
,
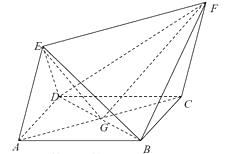
∵四边形 ![]() 为菱形,
为菱形,
∵ ![]() ,
,
在 ![]() 和
和 ![]() 中,
中,
![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() 平面
平面 ![]() ,
,
∵ ![]() 平面
平面 ![]() ,
,
∴平面 ![]() 平面
平面 ![]() ;
;
(2)
解法一:连接 ![]() ,∵
,∵ ![]() 面
面 ![]() 平面
平面 ![]() ,∴
,∴ ![]() ,
,
在平行四边形 ![]() 中,易知
中,易知 ![]() ,
,
∴ ![]() ,即
,即 ![]() ,又因为
,又因为 ![]() 为平面
为平面 ![]() 内的两条相交直线,所以
内的两条相交直线,所以 ![]() 平面
平面 ![]() ,所以点
,所以点 ![]() 到平面
到平面 ![]() 的距离为
的距离为 ![]() ,
,
∵ ![]() ,
,
∴三棱锥 ![]() 的体积为
的体积为 ![]() .
.
解法二:∵ ![]() ,∴点
,∴点 ![]() 到平面
到平面 ![]() 的距离为点
的距离为点 ![]() 到平面
到平面 ![]() 的距离的两倍,所以
的距离的两倍,所以 ![]() ,
,
作 ![]() ,∵平面
,∵平面 ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
∴ ![]() ,
,
∴三棱锥 ![]() 的体积为
的体积为 ![]() .
.
【解析】(1)做辅助线,连接EG,通过证明△EAD和△EAB全等,得到ED=EB,即EG⊥BD。四边形ABCD为菱形,则有AC⊥BD,故BD⊥平面ACFE,进而可以证明两个平面垂直。(2)连接FG,证明FG为点F到△BDE的距离,求出△BDE的面积,通过三棱锥公式即可求出三棱锥体积。

 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】近年来我国电子商务行业迎来篷布发展的新机遇,2015年双11期间,某购物平台的销售业绩高达918亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若将频率视为概率,某人在该购物平台上进行的5次购物中,设对商品和服务全好评的次数为随机变量X: ①求对商品和服务全好评的次数X的分布列(概率用组合数算式表示);
②求X的数学期望和方差.
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
( ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)