题目内容
直线x-y+m=0与圆x2+y2-2x-1=0有两个不同的交点的一个充分不必要条件为( ).
| A.m<1 | B.-3<m<1 | C.-4<m<2 | D.0<m<1 |
D
解析试题分析:联立直线与圆的方程得: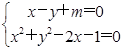 ,
,
消去y得:2x2+(2m-2)x+m2-1=0,由题意得:△=(2m-2)2-8(m2-1)=-4(m+1)2+16>0,
变形得:(m+3)(m-1)<0,解得:-3<m<1,
∵0<m<1是-3<m<1的一个真子集,∴直线与圆有两个不同交点的一个充分不必要条件是0<m<1.故选D.
考点:直线与圆相交的性质;以及充分必要条件的判断.

练习册系列答案
相关题目
设双曲线  ,离心率
,离心率  ,右焦点
,右焦点  ,方程
,方程  的两个实数根分别为
的两个实数根分别为  ,则点
,则点  与圆
与圆  的位置关系
的位置关系
| A.在圆内 | B.在圆上 | C.在圆外 | D.不确定 |
过点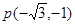 的直线l与圆
的直线l与圆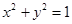 有公共点,则直线l的倾斜角的取值范围是
有公共点,则直线l的倾斜角的取值范围是
A.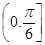 | B.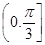 | C.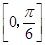  | D.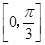 |
当曲线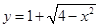
 与直线
与直线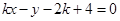 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )
A.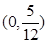 | B.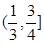 | C.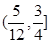 | D.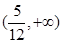 |
直线 :
: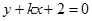 与曲线C:
与曲线C: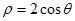 有交点,则
有交点,则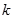 的取值范围是( )
的取值范围是( )
A.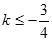 | B.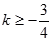 | C.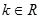 | D.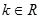 但 但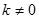 |
已知圆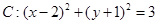 ,从点
,从点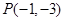 发出的光线,经
发出的光线,经 轴反射后恰好经过圆心
轴反射后恰好经过圆心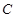 ,则入射光线的斜率为( )
,则入射光线的斜率为( )
A. | B. | C.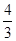 | D.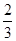 |
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2 ,2 ,2 ) ) | B.(- , , ) ) |
C.(-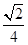 , ,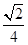 ) ) | D.(-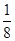 , ,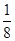 ) ) |
若圆心在x轴上、半径为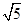 的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( )
的圆O位于y轴左侧,且与直线x+2y=0相切,则圆O的方程是( )
A.(x-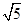 )2+y2=5 )2+y2=5 | B.(x+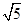 )2+y2=5 )2+y2=5 |
| C.(x-5)2+y2=5 | D.(x+5)2+y2=5 |
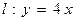 和点
和点 ,点
,点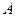 为第一象限内的点且在直线
为第一象限内的点且在直线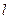 上,直线
上,直线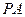 交
交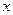 轴正半轴于点
轴正半轴于点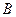 ,求△
,求△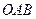 面积的最小值,并求当△
面积的最小值,并求当△