题目内容
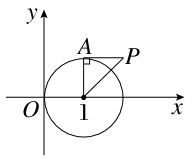
设A为圆(x-1)2+y2=1上的动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程是( )
| A.(x-1)2+y2=4 | B.(x-1)2+y2=2 |
| C.y2=2x | D.y2=-2x |
B
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
当曲线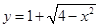
 与直线
与直线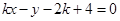 有两个相异的交点时,实数k的取值范围是( )
有两个相异的交点时,实数k的取值范围是( )
A.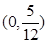 | B.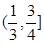 | C.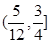 | D.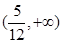 |
已知圆 截直线
截直线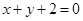 所得弦的长度为4,则实数
所得弦的长度为4,则实数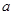 的值为( )
的值为( )
A.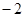 | B.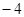 | C.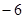 | D.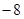 |
已知圆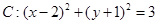 ,从点
,从点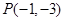 发出的光线,经
发出的光线,经 轴反射后恰好经过圆心
轴反射后恰好经过圆心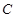 ,则入射光线的斜率为( )
,则入射光线的斜率为( )
A. | B. | C.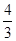 | D.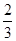 |
过点A(-1,0),斜率为k的直线,被圆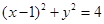 截得的弦长为2
截得的弦长为2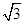 ,则k的值为( )。
,则k的值为( )。
A.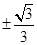 | B. | C.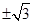 | D.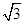 |
已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2 ,2 ,2 ) ) | B.(- , , ) ) |
C.(-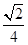 , ,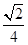 ) ) | D.(-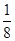 , ,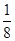 ) ) |
已知圆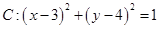 和两点
和两点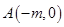 ,
,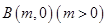 ,若圆
,若圆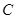 上存在点
上存在点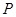 ,使得
,使得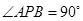 ,则
,则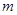 的最大值为( )
的最大值为( )
A. | B. | C.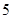 | D.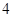 |
直线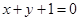 被圆
被圆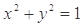 所截得的弦长为( )
所截得的弦长为( )
A.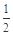 | B.1 | C.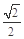 | D.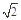 |
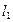 与直线
与直线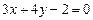 平行且与两坐标轴的正半轴围成的面积为12
平行且与两坐标轴的正半轴围成的面积为12  与直线
与直线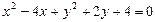 相切,求直线
相切,求直线