题目内容
（1-2x）6的展开式中x2项的系数是（ ）
| A、12 | B、54 | C、60 | D、160 |
考点：二项式系数的性质
专题：二项式定理
分析：先求出二项式展开式的通项公式，再令x的幂指数等于2，求得r的值，即可求得展开式中的x2项的系数．
解答：解：∵（1-2x）6的展开式的通项公式为Tr+1=
•（-2x）r，
令r=2，可得
×4=60，
故答案为：C．
| C | r 6 |
令r=2，可得
| C | 2 6 |
故答案为：C．
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=（x+a）2-7lnx+1在（1，+∞）上单调递增，则实数a的取值范围为（ ）
A、（
| ||
B、[
| ||
C、（-∞，
| ||
D、（-∞，-
|
设i是虚数单位，复数i3+
=（ ）
| 2i |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
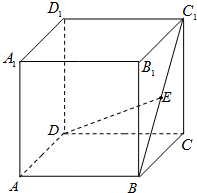如图，在正方体ABCD-A1B1C1D1中，E为BC1的中点，则DE与面BCC1B1所成角的正切值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在(x2-
)5的展开式中，x的系数为（ ）
| 1 |
| x |
| A、10 | B、-10 |
| C、20 | D、-20 |
如图，D、E分别是AB、AC上两点，CD与BE相交于点O，下列条件中不能使△ABE和△ACD相似的是（ ）| A、∠B=∠C | B、∠ADC=∠AEB | C、BE=CD，AB=AC | D、AD：AC=AE：AB |
已知，在Rt△ABC中，CD为斜边上的高，CE平分∠BCD，交AB于点E．求证：AE2=AD•AB．矩阵A=
，向量
=
，则A10
=（ ）
|
| α |
|
| α |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|