题目内容
16.设函数f(x)=$\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$(1)证明:函数f(x)是奇函数;
(2)证明:函数f(x)在R上是增函数.
分析 (1)利用奇函数的定义,即可证明;
(2)利用导数大于0,即可证明.
解答 证明:(1)函数的定义域为R,
∴f(x)=$\frac{{2}^{x}-1}{2({2}^{x}+1)}$
∴f(-x)=$\frac{{2}^{-x}-1}{2({2}^{-x}+1)}$=-$\frac{{2}^{x}-1}{2({2}^{x}+1)}$=-f(x),
∴函数f(x)是奇函数;
(2)∵f(x)=$\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$
∴f′(x)=-$\frac{{-2}^{x}ln2}{({2}^{x}+1)^{2}}$>0
∴函数f(x)在R上是增函数.
点评 本题考查函数的单调性、奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
6.已知函数f(x)=sin2x+cos2x,将f(x)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再将所得的图象向右平移$\frac{π}{4}$个单位,得到的函数y=g(x)的图象.则函数y=g(x)的图象的对称中心不可能是( )
| A. | (-$\frac{3π}{16}$,0) | B. | ($\frac{3π}{16}$,0) | C. | ($\frac{7π}{16}$,0) | D. | ($\frac{15π}{16}$,0) |
11.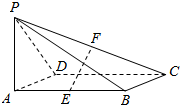 如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.
(1)求证:EF⊥PD;
(2)求点E到平面PDC的距离.
 如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD=1,AB=$\sqrt{2}$,点E,F分别为AB、PC中点.(1)求证:EF⊥PD;
(2)求点E到平面PDC的距离.
8.已知R是实数集,集合P={m∈R|mx2+4mx-4<0对?x∈R都成立},Q={x|y=ln(x2+2x)},则(∁RP)∩(∁RQ)=( )
| A. | {x|-2≤x≤-1} | B. | {x|-2≤x≤-1或x=0} | C. | {x|-2≤x<-1} | D. | {x|-2≤x<-1或x=0} |
5.已知函数$f(x)=\left\{\begin{array}{l}(a-3)x+2,x≤1\\{x^{1-a}},x>1\end{array}\right.$是(-∞,+∞)上的减函数,那么a的取值范围是( )
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (2,3) |
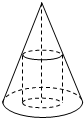 如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.
如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.