题目内容
2010年上海世博会大力倡导绿色出行,并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量.某游客非常支持这一方案,计划在游园期间种植n棵树,已知每棵树是否成活互不影响,成活率为p(0<p<1),设ξ表示他所种植的树中成活的棵数,ξ的数学期望为Eξ,方差为Dξ.(1)若n=1,求Dξ的最大值;
(2)已知Eξ=3,标准差?ξ=
| ||
| 2 |
分析:(1)ξ表示他所种植的树中成活的棵数,当n=1,ξ的可能取值是0,1,写出ξ的分布列,根据分布列做出期望值,代入方差的公式求出方差,根据二次函数的最值求出结果.
(2)根据每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),根据Eξ=np,Dξ=npq=np(1-p),求出P的值,ξ表示他所种植的树中成活的棵数,则变量的可能取值是0,1,2,3,4,根据独立重复试验概率公式写出变量的分布列.
(2)根据每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),根据Eξ=np,Dξ=npq=np(1-p),求出P的值,ξ表示他所种植的树中成活的棵数,则变量的可能取值是0,1,2,3,4,根据独立重复试验概率公式写出变量的分布列.
解答:解:(1)由题意知ξ表示他所种植的树中成活的棵数,
当n=1,ξ=0,1,于是ξ的分布列为
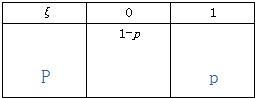
∴Eξ=0×(1-p)+1×p=p.
∴Dξ=(0-p)2•(1-p)+(1-p)2•p=p-p2=-(p-
)2+
即当p=
时,Dξ有最大值
.
(2)每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),
∴Eξ=np,Dξ=npq=np(1-p),
∴np=3,
=
,
∴p=
,n=4.
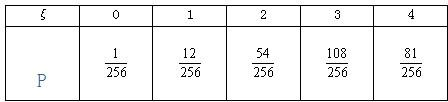
∴P(ξ=k)=
(
)k(1-
)4-k(k=0,1,2,3,4),
∴ξ的分布列为
当n=1,ξ=0,1,于是ξ的分布列为

∴Eξ=0×(1-p)+1×p=p.
∴Dξ=(0-p)2•(1-p)+(1-p)2•p=p-p2=-(p-
| 1 |
| 2 |
| 1 |
| 4 |
即当p=
| 1 |
| 2 |
| 1 |
| 4 |
(2)每棵树是否成活互不影响,成活率为p得到ξ~B(n,p),
∴Eξ=np,Dξ=npq=np(1-p),
∴np=3,
| np(1-p) |
| ||
| 2 |
∴p=
| 3 |
| 4 |
∴P(ξ=k)=
| C | k 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴ξ的分布列为

点评:本题考查离散型随机变量的分布列,考查n次独立重复试验恰好发生k次的实验,考查二次函数的最值问题,考查利用概率知识解决实际问题,是一个综合题目.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 为迎接2010年上海世博会,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为5cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
为迎接2010年上海世博会,要设计如图的一张矩形广告,该广告含有大小相等的左中右三个矩形栏目,这三栏的面积之和为60000cm2,四周空白的宽度为10cm,栏与栏之间的中缝空白的宽度为5cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小. 某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.