题目内容
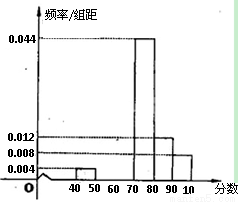
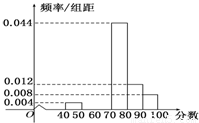
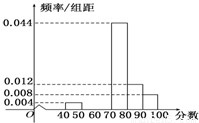
 某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
某社区为了选拔若干名2010年上海世博会的义务宣传员,从社区300名志愿者中随机抽取了50名进行世博会有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.(1)求第二组、第三组的频率并补充完整频率分布直方图;
(2)由所抽取志愿者的成绩分布,估计该社区有多少志愿者可以入选为义务宣传员.
分析:(1)先求出第二组、第三组的人数和,以及第一组的人数,设公差为d,根据第一、二、三组的人数依次构成等差数列可得第二组、第三组的人数和,从而求出所求,作出频率分布直方图即可;
(2)先根据矩形面积表示频率求出成绩不低于66分的频率,然后利用样本估计总体得到可以入选为义务宣传员的人数.
(2)先根据矩形面积表示频率求出成绩不低于66分的频率,然后利用样本估计总体得到可以入选为义务宣传员的人数.
解答:解:(1)二、三两组的人数和为50-(0.004+0.044+0.012+0.008)×10×50=16
设公差为d,第一组人数为0.004×10×50=2人
∴2+d+2+2d=16
解得d=4
∴第二组的频率是
=0.12;第三组的频率是
=0.20
补全频率分布直方图如下图所示
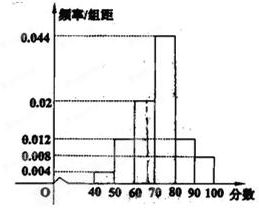
(2)成绩不低于66分的频率为(
×0.02+0.044+0.012+0.008)×10=0.72
估计可成为义务宣传员的人数为0.72×300=216人
设公差为d,第一组人数为0.004×10×50=2人
∴2+d+2+2d=16
解得d=4
∴第二组的频率是
| 2+4 |
| 50 |
| 2+8 |
| 50 |
补全频率分布直方图如下图所示

(2)成绩不低于66分的频率为(
| 4 |
| 10 |
估计可成为义务宣传员的人数为0.72×300=216人
点评:本题主要考查频率分布直方图,以及用样本估计总体、等可能事件的概率,同时考查了作图能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
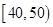 ,第二组
,第二组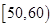 ,
,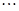 ,第六组
,第六组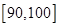 ,第一、二、三组的人数依次构成等差数列,右图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
,第一、二、三组的人数依次构成等差数列,右图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.