Question

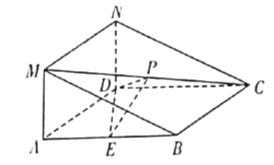
【题目】已知平面上两定点M（0，﹣2）、N（0，2），P为一动点，满足||||

（I）求动点P的轨迹C的方程；

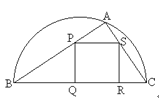
（II）若A、B是轨迹C上的两不同动点，且λ.分别以A、B为切点作轨迹C的切线，设其交点Q，证明为定值.

Answer 1

【答案】（I）x2＝8y

（II）见解析

【解析】

（I）先设P（x，y），求动点P的轨迹C的方程，即寻找x，y之间的关系，结合向量的坐标运算即可得到．

（II）先设出A，B两点的坐标，利用向量关系及向量运算法则，用A，B的坐标表示出，最后看其是不是定值即可．

（I）设P（x，y）.

由已知 （x，y+2），（0，4），（﹣x，2﹣y），

4y+8.

||||＝4

∵||||

∴4y+8＝4整理，得x2＝8y

即动点P的轨迹C为抛物线，其方程为x2＝8y.

（II）由已知N（0，2）.

即得（﹣x1，2﹣y1）＝λ（x2，y2﹣2）

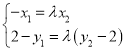
设A（x1，y1），B（x2，y2）.由λ

即得（﹣x1，2﹣y1）＝λ（x2，y2﹣2），

∴﹣x1＝λx2…（1），

2﹣y1＝λ（y2﹣2）…（2）

将（1）式两边平方并把x12＝8y1，x2/span>2＝8y2代入得y1＝y2

解得 y1＝2λ，y2，

且有x1x2＝﹣λx22＝﹣8λy2＝﹣16.

抛物线方程为 y＝，求导得y′x.

所以过抛物线上A、B两点的切线方程分别是 yx1（x﹣x1）+y1，yx2（x﹣x2）+y2，

即yx1xx12，yx2xx22

解出两条切线的交点Q的坐标为 （，）＝（，﹣2）

所以 （，﹣4）（x2﹣x1，y1﹣y2）

（x22﹣x12）﹣4（x22x12）＝0

所以 为定值，其值为0.