题目内容
(本小题满分12分)
已知函数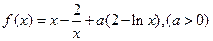 ,讨论
,讨论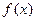 的单调性。
的单调性。
已知函数
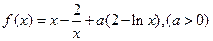 ,讨论
,讨论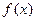 的单调性。
的单调性。当 时,
时,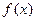 在
在 上是增函数;
上是增函数;
当 时,
时,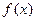 在
在 上是增函数;
上是增函数;
当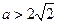 时,
时,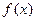 在
在 上单调递增,在
上单调递增,在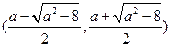 是上单调递减, 在
是上单调递减, 在 上单调递增。
上单调递增。
 时,
时,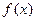 在
在 上是增函数;
上是增函数;当
 时,
时,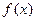 在
在 上是增函数;
上是增函数;当
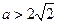 时,
时,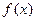 在
在 上单调递增,在
上单调递增,在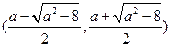 是上单调递减, 在
是上单调递减, 在 上单调递增。
上单调递增。本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。
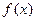 的定义域是(0,+
的定义域是(0,+ ),
), 。
。
设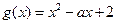 ,二次方程
,二次方程 的判别式
的判别式 。
。
①当 ,即
,即 时,对一切
时,对一切 都有
都有 ,此时
,此时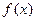 在
在 上是增函数。
上是增函数。
②当 ,即
,即 时,仅对
时,仅对 有
有 ,对其余的
,对其余的 都有
都有 ,此时
,此时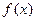 在
在 上也是增函数。
上也是增函数。
③当 ,即
,即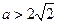 时,
时,
方程 有两个不同的实根
有两个不同的实根 ,
, ,
, 。
。
此时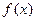 在
在 上单调递增,在
上单调递增,在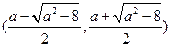 是上单调递减, 在
是上单调递减, 在 上单调递增。
上单调递增。
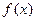 的定义域是(0,+
的定义域是(0,+ ),
), 。
。设
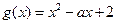 ,二次方程
,二次方程 的判别式
的判别式 。
。①当
 ,即
,即 时,对一切
时,对一切 都有
都有 ,此时
,此时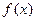 在
在 上是增函数。
上是增函数。②当
 ,即
,即 时,仅对
时,仅对 有
有 ,对其余的
,对其余的 都有
都有 ,此时
,此时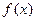 在
在 上也是增函数。
上也是增函数。③当
 ,即
,即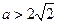 时,
时,方程
 有两个不同的实根
有两个不同的实根 ,
, ,
, 。
。 |  |  | 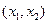 |  |  |
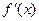 | + | 0 | _ | 0 | + |
 | 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
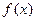 在
在 上单调递增,在
上单调递增,在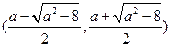 是上单调递减, 在
是上单调递减, 在 上单调递增。
上单调递增。
练习册系列答案
相关题目
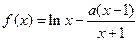 .
.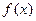 在
在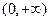 上为单调增函数,求
上为单调增函数,求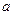 的取值范围;
的取值范围;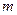 ,
,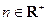 ,且
,且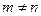 ,求证:
,求证: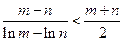 .
.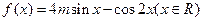 ,若函数
,若函数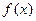 的最大值为3,求实数m的值。
的最大值为3,求实数m的值。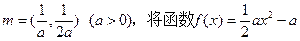 的图象按向量m平移后得到函数
的图象按向量m平移后得到函数 的图象。
的图象。 上的最小值为
上的最小值为 的最大值。
的最大值。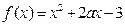 的最小值为负数,并求出当最小值为-4时的
的最小值为负数,并求出当最小值为-4时的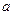 值.
值.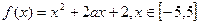 .
.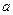 的范围,使
的范围,使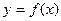 在区间
在区间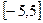 上是单调函数。 (2)求
上是单调函数。 (2)求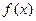 的最小值
的最小值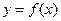 是奇函数,对于任意
是奇函数,对于任意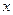 、
、 R都有
R都有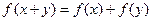 ,且当
,且当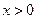 时,
时,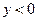 ,
,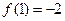 ,求函数
,求函数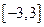 上的最大值和最小值.
上的最大值和最小值.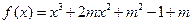 (其中
(其中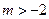 )
) ,求函数
,求函数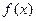 的单调区间及极小值;
的单调区间及极小值;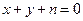 对任意的
对任意的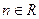 都不是曲线
都不是曲线 的切线,求
的切线,求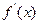 的最小值及实数
的最小值及实数 的取值范围.
的取值范围.