题目内容
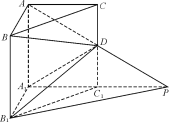
【题目】如图，直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形，高AA1= 
，点A是平面α内的一个定点，AA1与α所成角为 
，点C1在平面α内的射影为P，当四棱柱ABCD﹣A1B1C1D1按要求运动时（允许四棱柱上的点在平面α的同侧或异侧），点P所经过的区域的面积= ． 
【答案】
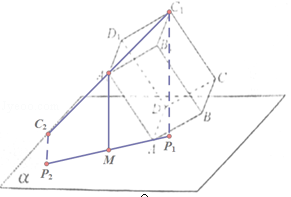
【解析】解：当长方体绕A1A转的时候，C1C形成一个圆柱，过C1往平面α作垂线垂足P，就形成一个椭圆，其短轴为P1P2= 
，长轴为 
的y型的椭圆，其中心A点在平面α上的射影M．
当AA1绕着A点转时，则椭圆就以A为圆心， 
为半径的圆上运动，其扫过的区域为一个圆环，外径为 
，内径为 
，
所以面积为：[（ ）2﹣ 
]π=
故填： ．
【考点精析】利用棱柱的结构特征对题目进行判断即可得到答案，需要熟知两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面是与底面全等的多边形．
练习册系列答案
相关题目
【题目】某大学准备在开学时举行一次大学一年级学生座谈会，拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加，各学院邀请的学生数如下表所示：
学院 | 机械工程学院 | 海洋学院 | 医学院 | 经济学院 |
人数 | 4 | 6 | 4 | 6 |
（Ⅰ）从这20名学生中随机选出3名学生发言，求这3名学生中任意两个均不属于同一学院的概率；
（Ⅱ）从这20名学生中随机选出3名学生发言，设来自医学院的学生数为ξ，求随机变量ξ的概率分布列和数学期望．