Question

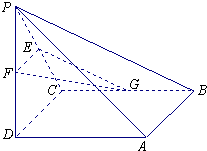（2011•孝感模拟）如图所示，四棱锥P-ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别为PC、PD、BC的中点．
（Ⅰ）求证：PA⊥EF；
（Ⅱ）求证：FG∥平面PAB．

Answer 1

分析：（Ⅰ）由于EF∥CD，要证明PA⊥EF，只要证CD⊥PA，结合已知，PD⊥平面ABCD，可得CD⊥PD．由ABCD为正方形，可得CD⊥AD．则可得CD⊥平面PAD可证
（Ⅱ）（法一）利用线面平行的判定定理，要证FG∥平面PAB．只要证明FG平行于平面PAB内的一条直线，结合题目特点考虑取PA的中点H，则由中位线的性质可知四边形FHBG是平行四边形．从而可得FG∥HB
（法二）利用面面平行的性质，要证FG∥平面PAB．只要证明平面EFG∥平面PAB即可

解答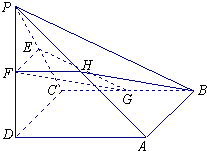：证明：（Ⅰ）∵PD⊥平面ABCD，CD?平面ABCD，
∴CD⊥PD．
又ABCD为正方形，
∴CD⊥AD．
∵PD∩AD=D，
∴CD⊥平面PAD．-----------（3分）
∵PA?平面PAD，
∴CD⊥PA．
∵EF∥CD，
∴PA⊥EF．----------（6分）
（Ⅱ）取PA的中点H，连接FH，HB，
∵F，H，G分别是PD，PA，BC的中点，且ABCD为正方形，
∴FH∥AD，BG∥AD，
且FH=

1

2

AD，BG=

1

2

AD
∴FH∥BG，且FH=BG．
∴四边形FHBG是平行四边形．
∴FG∥HB．----------（10分）
又∵FG在平面PAB外，HB?平面PAB．
∴FG∥平面PAB．----------（12分）
（法二）∵F，H，G分别是PD，PA，BC的中点，且ABCD为正方形，
∴EF∥AB，EG∥PB，
由线面平行的判定定理可知，EF∥平面PAB，EG∥平面PAB
∵EF∩EG=E
∴根据平面与平面平行的判定定理可得，平面EFG∥平面PAB
∵FG⊆平面EFG
∴FG∥平面PAB．

点评：本题 主要考查了线面垂直，线面平行与线线垂直、线线平行的相互转化关系的应用，证明线面垂直关键是证明直线与面内的两条相交直线垂直；证明线面平行关键是证明已知直线与面内一条直线平行即可