题目内容
 (2011•孝感模拟)如图,正四面体ABCD的外接球球心为D,E是BC的中点,则直线OE与平面BCD所成角的正切值为
(2011•孝感模拟)如图,正四面体ABCD的外接球球心为D,E是BC的中点,则直线OE与平面BCD所成角的正切值为
| ||
| 2 |
| ||
| 2 |
分析:欲求直线OE与平面BCD所成角的正切值,需先找到直线在平面上的射影的位置,直线与它的射影所成角即直线OE与平面BCD所成角,根据四面体ABCD为正四面体,可得O点在平面BCD上的射影在DE上,在根据正四面体的性质,即可求∠OED的正切值.
解答:解:设正四面体ABCD的棱长为a,连接AE,DE,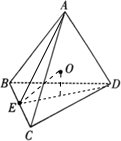
∵四面体ABCD为正四面体,E为BC的中点,
∴AE=DE=
a,O点在平面ADE上,且OE等分∠AED
过O作OH垂直平面BCD,交平面BCD与H点,则H落在DE 上,
∴∠OED为直线OE与平面BCD所成角,∠OED=
∠AED
在△AED中,cos∠AED=
=
=
,
∴cos2∠OED=cos
∠AED=
=
,sin2∠OED=
∴tan2∠OED=
,tan∠OED=
故答案为

∵四面体ABCD为正四面体,E为BC的中点,
∴AE=DE=
| ||
| 2 |
过O作OH垂直平面BCD,交平面BCD与H点,则H落在DE 上,
∴∠OED为直线OE与平面BCD所成角,∠OED=
| 1 |
| 2 |
在△AED中,cos∠AED=
| AE2+DE2-AD2 |
| 2AE•DE |
(
| ||||||||
2
|
=
| 1 |
| 3 |
∴cos2∠OED=cos
| 1 |
| 2 |
1+
| ||
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∴tan2∠OED=
| 1 |
| 2 |
| ||
| 2 |
故答案为
| ||
| 2 |
点评:本题主要考查了正四面体中的线面角的求法,综合考查了学生的空间想象力,公式的运用,以及计算能力.

练习册系列答案
相关题目
 (2011•孝感模拟)已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( )
(2011•孝感模拟)已知f(x)=2sin(ωx+φ)的部分图象如图所示,则f(x)的表达式为( )