题目内容
【题目】已知函数![]() ,
,![]() 是
是![]() 的一个极值点
的一个极值点
(1)求实数![]() 的值,并证明:当
的值,并证明:当![]() 时,
时,![]() 恒成立;
恒成立;
(2)若函数![]() ,试讨论函数
,试讨论函数![]() 的零点个数
的零点个数
【答案】(1)2;证明见解析(2)![]() 时,0个;
时,0个;![]() 时,1个;
时,1个;![]() 时,2个
时,2个
【解析】
(1)求得函数的导数,由题意可得![]() (1)
(1)![]() ,解方程可得
,解方程可得![]() 的值,求得
的值,求得![]() 的导数,可得单调性和极值点,考虑极小值大于0,即可得证;
的导数,可得单调性和极值点,考虑极小值大于0,即可得证;
(2)由方程![]() 分离参数得
分离参数得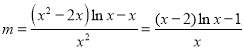 ,转化为研究函数的单调性和极值,利用函数大致图象求
,转化为研究函数的单调性和极值,利用函数大致图象求![]() 与
与![]() 交点即可.
交点即可.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() 的导数为
的导数为![]() ,
,
因为![]() 是
是![]() 的一个极值点,
的一个极值点,
所以![]() (1)
(1)![]() ,
,
解得![]() ;
;
故![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取得极小值,
取得极小值,
因为![]() (1)
(1)![]() ,所以当
,所以当![]() 时,
时,![]() 恒成立.
恒成立.
(2)令![]() ,得
,得![]() ,即
,即![]()
整理得![]() ,
,
显然![]() ,分离参数得
,分离参数得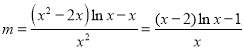
记![]()
则![]()
记![]() 则
则![]() 恒成立,
恒成立,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,
所以当![]() 时,
时,![]() 即
即![]() 所以函数
所以函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() ,所以函数
,所以函数![]() 单调递增.
单调递增.
又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 的最小值为
的最小值为![]() .
.
函教![]() 的零点个数,即为函数
的零点个数,即为函数![]() 和函数
和函数![]() 的图象的交点个数,
的图象的交点个数,
所以当![]() 时,两函数图象没有交点,函数
时,两函数图象没有交点,函数![]() 有一个零点;
有一个零点;
当![]() 时,两函数图象有两个交点,函数
时,两函数图象有两个交点,函数![]() 有两个零点.
有两个零点.

练习册系列答案
相关题目
【题目】为了普及环保知识,增强环保意识,某大学从理工类专业的![]() 班和文史类专业的
班和文史类专业的![]() 班各抽取
班各抽取![]() 名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
名同学参加环保知识测试,统计得到成绩与专业的列联表:( )
优秀 | 非优秀 | 总计 | |
| 14 | 6 | 20 |
| 7 | 13 | 20 |
总计 | 21 | 19 | 40 |
附:参考公式及数据:
(1)统计量:![]() ,(
,(![]() ).
).
(2)独立性检验的临界值表:
| 0.050 | 0.010 |
| 3.841 | 6.635 |
则下列说法正确的是
A. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
B. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关
C. 有![]() 的把握认为环保知识测试成绩与专业有关
的把握认为环保知识测试成绩与专业有关
D. 有![]() 的把握认为环保知识测试成绩与专业无关
的把握认为环保知识测试成绩与专业无关