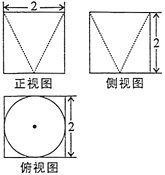
题目内容
【题目】已知点A,B关于坐标原点O对称,![]() ,以M为圆心的圆过A,B两点,且与直线
,以M为圆心的圆过A,B两点,且与直线![]() 相切,若存在定点P,使得当A运动时,
相切,若存在定点P,使得当A运动时,![]() 为定值,则点P的坐标为( )
为定值,则点P的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设M的坐标为(x,y),然后根据条件得到圆心M的轨迹方程为x2=﹣y,把|MA|﹣|MP|转化后再由抛物线的定义求解点P的坐标.
解:∵线段AB为⊙M的一条弦O是弦AB的中点,∴圆心M在线段AB的中垂线上,
设点M的坐标为(x,y),则|OM|2+|OA|2=|MA|2,
∵⊙M与直线2y﹣1=0相切,∴|MA|=|y![]() |,
|,
∴|y![]() |2=|OM|2+|OA|2=x2+y2
|2=|OM|2+|OA|2=x2+y2![]() ,
,
整理得x2=﹣y,
∴M的轨迹是以F(0,![]() )为焦点,y
)为焦点,y![]() 为准线的抛物线,
为准线的抛物线,
∴|MA|﹣|MP|=|y![]() |﹣|MP|
|﹣|MP|
=|y![]() |﹣|MP|
|﹣|MP|![]() |MF|﹣|MP|
|MF|﹣|MP|![]() ,
,
∴当|MA|﹣|MP|为定值时,则点P与点F重合,即P的坐标为(0,![]() ),
),
∴存在定点P(0,![]() )使得当A运动时,|MA|﹣|MP|为定值.
)使得当A运动时,|MA|﹣|MP|为定值.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目